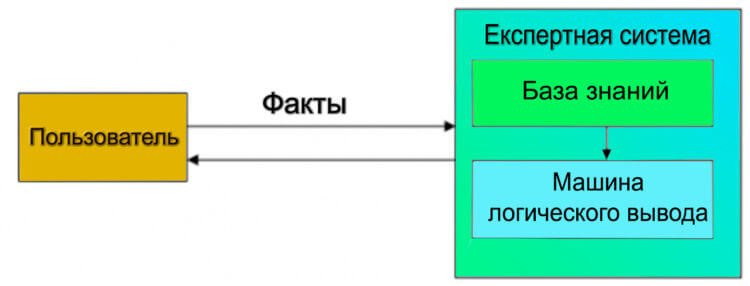
Пропозициональная логика в представлении знаний
Для манипулирования выражениями используется символическая логика, которая имеет название - пропозициональная логика. В частности, пропозициональная логика может использоваться для манипулирования логическими переменными, обозначающие высказывания.
Модель представления знаний с применением пропозициональной логики часто представляется в научной литературе, как вычисление выражений. 
Все предложения естественного языка делятся на четыре основных типа:
- повелительные,
- вопросительные,
- восклицательные,
- повествовательные.
Пропозициональная логика рассматривает повествовательные предложения. Они могут разделяются на истинные и ложные. Предложение, истинное значение которого может быть определено, называется утверждением или заключением.
Утверждение принято называть также закрытым предложением, поскольку его значение не подлежит обсуждению, учитывая его истинность. Предложения, об истинности которых невозможно дать однозначный ответ, называются открытыми предложениями.
Например, открытым является предложение «Качество заемщика определяется наличием постоянного места работы», поскольку оно является истинным для одних людей и ошибочным для других. Неоднозначностьютакого рода невозможно эффективно оперировать с помощью пропозициональной логики.
Подобные проблемы решаются с использованием нечеткой логики. Вычисление выражений осуществляется на основе логических связок к отдельным высказываниям, в результате применения которых формируются сложные выражения. Для этого применяются логические связи, наиболее распространенные из которых, следующие:
- AND (Λ) - конъюнкция;
- OR (V) - дизъюнкция;
- если ... то ... (→) - условная операция;
- если и только если (↔) - двусторонняя условная операция;
- NOT (~) - отрицание.
Конъюнкция осуществляется благодаря применению логического «И» между двумя высказываниями. Ее результат - сложный выражение будет истинным, если истинны оба выражения.
Дизъюнкция осуществляется благодаря применению логического «ИЛИ» между двумя высказываниями. Ее результат будет истинным, если истинный хотя бы один из этих высказываний. Условная операция аналогична форме IF-THEN продукционных правил.
Например, следующее выражение:
IF клиент имеет постоянный доход THEN выдать кредитможет быть представлен в следующей форме: p → q, где применяются следующие обозначения: р - клиент имеет постоянный доход, q - выдать кредит.
Двусторонняя условная операция г ↔ q эквивалентна выражению: (P → q) Λ (q → г) Она истинна только тогда, когда р и q имеют одновременно истинное или ложное значение. Все операции пропозициональной логики, которые были рассмотрены, относятся к бинарным.
В отличие от них, операция отрицания является унарной, поскольку применяется к одному выражению. Она имеет высокий приоритет по сравнению с другими операциями. Сущность логических связок хорошо демонстрирует их применения для формализованного описания таких логических понятий, как тавтология и противоречие.
Тавтология - это сложное выражение, которое всегда является истинным, независимо от того, истинные или ложные отдельные высказывания, из которых он состоит.
Примером тавтологии может быть выражение: «Начальник всегда прав, поскольку он никогда не может не иметь смысла». В отличие от фактов, которые могут быть в реальном мире истинными или нет, тавтология всегда, в чисто логическом смысле, истинная, поскольку ссылается для доказательства на саму себя.
А противоречие представляет собой сложное выражение, которое всегда является ошибочным. Высказывания, которые не являются, ни тавтологией, ни противоречием, в пропозициональной логике называются контингентными.
Тавтологии и противоречия называются, соответственно, аналитически истинными и аналитически ложными высказываниями, поскольку истинность их значений может быть определено исключительно на основании анализа формы.
В частности, истинное значение для выражения: р V ~ г показывает, что это - тавтология, а для выражения: г Λ ~ р, что это - противоречие. Множество логических связок называется адекватной, если с помощью связок, взятых исключительно из этого множества, можно представить любую функцию истины.
Примером адекватных множеств можно отнести множества {~, Λ, V}, {~, Λ}, {~, V}. Несмотря на то, что пропозициональная логика очень полезна, в представлении знаний она имеет определенные ограничения.
Основная проблема заключается в том, что пропозициональная логика может применяться только с полным выражением. Это означает, что с ее помощью нельзя исследовать внутреннюю структуру высказывания.
Например, пропозициональная логика не позволяет доказать обоснованность приведенного ранее силлогизма в отношении смертности преподавателя, (подробнее: Формальная логика Аристотеля).