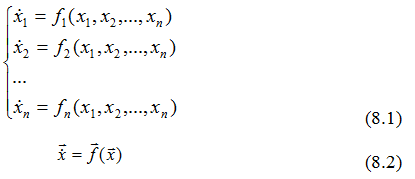Использования оборотных систем для исследования устойчивости нелинейных динамических систем.
Часто динамические системы имеют оборотную во времени симметрию в том смысле, что их поведение не зависит от направления времени.
Так, например, нить, на которой подвешен маятник, одинакова независимо от того, колеблется маятник вперед или назад.
Планарная (плоская) динамическая система 
Заметим, что во многих динамических системах х представляет перемещения, а y представляет скорость, так как y=x'. Соответственно, изменение знака t также изменяет знак y, но не x.
Свойство оборотной системы
Если x(t), y(t) является решением системы, то решением является и x(t), y(t). Это означает, что любая траектория системы, находящейся над осью х (или слева от оси y) должна иметь двойника, который получают отражением относительно оси х (или оси y) и который отличается по направлению времени.
То есть, фазовый портрет системы симметричен относительно оси х (или оси y). Что это нам дает в понимании долгосрочного поведения нелинейной системы? Рассмотрим траекторию, начинающуюся на оси х справа от точки равновесия. Эта траектория кружит вокруг точки равновесия и, в конце концов, пересечет ось слева от точки равновесия.
По свойству обратимой системы, должна существовать соответствующая траектория, полученная с помощью отображения относительно оси х с той же конечной точкой, только оборотная во времени. Вместе эти две траектории образуют замкнутую орбиту.
Итак, точка равновесия является центром. Аналогичные рассуждения справедливы и относительно оси у.
Теорема: если оборотная система имеет точку равновесия, которой соответствует линеаризация с центром, нелинейная система должна иметь нелинейный центр. Таким образом, определение обратимости системы может быть полезным при доказательстве существования нелинейного центра.