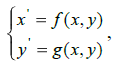Катастрофа "Сборка"
Как рассматривалось в посте о бифуркационных поверхностях вне сборки есть только один корень, и он всегда отвечает минимуму потенциала f(x,r).
Внутри области есть три действительных корня: один из них соответствует максимуму (неустойчивое состояние), и два - минимуму, что можно проверить, исследуя вторую производную функции f. Заштрихованная область является областью катастроф, а граница - бифуркационных множество, где локальный минимум исчезает.
Как это происходит, можно увидеть на рис. 1, где в точках 3 и 7 на границе области исчезающие минимумы функции сливаются, образуя точку перегиба. Ось r1 (при r1<0 является конфликтной множеством, где существуют два минимума равной глубины. В случае сборки параметр r1 носит название «расщепляя множителя», а r2 - «нормального множителя» (Зиман, 1977).
Основанием для выбора такого наименования является то обстоятельство, что именно величина r1 определяет, траектория будет лежать в области складки поверхности: если r1>0. поверхность однозначна, тогда как в случае r1<0 она двусмысленна: с изменением же параметра r2 переменная х меняется монотонно и непрерывно, за исключением прыжков в точках бифуркации. 

Область действия теории катастроф ограничена упрощая предположениями относительно системы уравнений, описывающих поведение системы. Следовательно, предметом изучения теории катастроф является классификация состояний равновесия градиентных систем, которые могут проявляться как внезапные скачки - катастрофы - в поведении динамической системы.
Предположения теории катастроф
Основными предположениями теории катастроф являются:
- Система является динамической, т.е. ее состояние меняется во времени.
- Принцип максимального промедления: система стремится сохранять свое состояние как можно дольше.
- Текущее состояние системы зависит от того, каким образом система пришла в это состояние.
- Траектории системы необратимо, то есть при изменении управляющих параметров системы в точности противоположным образом система не обязательно дойдет начального состояния.