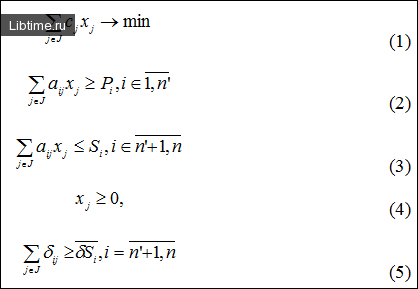Переход к хаосу через бифуркации
К хаосу системы могут переходить разными путями. Среди последних выделяют бифуркации, что изучает теория бифуркаций.
Бифуркация
Бифуркация (от лат. Bifurcus - раздвоенный) представляет собой процесс качественного перехода от состояния равновесия к хаосу через последовательное очень малое изменение (например, удвоение Фейгенбаума при бифуркации удвоения) периодических точек.
Обязательно необходимо отметить, что происходит качественное изменение свойств системы, т.н. катастрофический скачок. Момент прыжка (раздвоение при бифуркации удвоения) происходит в точке бифуркации. Хаос может возникнуть через бифуркацию, что показал Митчел Фейгенбаум (Feigenbaum).
При создании собственной теории о фракталах Фейгенбаум, в основном, анализировал логистическое уравнение: Xn+1=CXn - С(Хn)2, где С - внешний параметр. Откуда вывод, что при некоторых ограничениях во всех подобных уравнениях происходит переход от равновесного состояния к хаосу.
Пример бифуркации
Ниже рассмотрен классический биологический пример этого уравнения.
Например, изолированно живет популяция особей нормированной численностью Xn. Через год появляется потомство численностью Xn +1. Рост популяции описывается первым членом правой части уравнения (СХn), где коэффициент С определяет скорость роста и является определяющим параметром.
Ущерб животных (за счет перенаселенности, недостатка пищи и т.п.) определяется вторым, нелинейным членом С(Хn)2. Результатом расчетов являются следующие выводы:
- При С<1 популяция с ростом n вымирает;
- В области 1<С<3 численность популяции приближается к постоянному значению Х0=1-1/С, что является областью стационарных, фиксированных решений. При значении C=3 точка бифуркации становится отталкивающей фиксированной точкой. С этого момента функция уже никогда не сходится к одной точке. До этого точка была притягивающая фиксированная;
- В диапазоне 3 <С
- При C> 3.57 происходит перекрывание областей различных решений (они как бы закрашиваются) и поведение системы становится хаотическим.
Отсюда вывод - заключительным состоянием физических систем, эволюционируют, является состояние динамического хаоса. Зависимость численности популяции от параметра С приведена на следующем рисунке. 
Динамические переменные Xn принимают значения, сильно зависят от начальных условий. При проведенных на компьютере расчетах даже для очень близких начальных значений С итоговые значения могут резко отличаться.
Более того, расчеты становятся некорректными, так как начинают зависеть от случайных процессов в самом компьютере (скачки напряжения и т.п.).
Таким образом, состояние системы в момент бифуркации является крайне неустойчивым и бесконечно малое воздействие может привести к выбору дальнейшего пути движения, а это, как мы уже знаем, является главным признаком хаотической системы (существенная зависимость от начальных условий).
Фейгенбаум установил универсальные закономерности перехода к динамическому хаосу при удвоении периода, которые были экспериментально подтверждены для широкого класса механических, гидродинамических, химических и других систем. Результатом исследований Фейгенбаум стало т.н. «Дерево Фейгенбаума». 
Обозначим через 
Разница значений, соответствующих двум последовательным бифуркация, уменьшается каждый раз примерно с одинаковым коэффициентом: 

Понятие бифуркации
Что же такое бифуркации в обыденности. Как мы знаем из определения, бифуркации возникают при переходе системы от состояния видимой стабильности и равновесия к хаосу.
Примерами таких переходов являются дым, вода и много других самых обычных природных явлений. Так, что поднимается вверх дым сначала выглядит как упорядоченный столб.
Фактически первый переход от стабильности к некоторой форме видимой упорядоченности, но уже изменчивости, происходит в первой точке бифуркации. Далее количество бифуркаций увеличивается, достигая огромных величин. С каждой бифуркацией функция турбулентности дыма приближается к хаосу.
С помощью теории бифуркаций можно предсказать характер движения, возникающего при переходе системы в качественно иное состояние, а также область существования системы и оценить ее устойчивость. К сожалению, само существование теории хаоса трудно совместимо с классической наукой.
Конечно научные идеи проверяются на основании предсказаний и их сверки с реальными результатами. Однако, как мы уже знаем, хаос непредсказуем, когда изучаешь хаотическую систему, то можно прогнозировать только модель ее поведения.
Поэтому с помощью хаоса не только нельзя построить точный прогноз, но и, соответственно, проверить его. Однако это не должно говорить о неверности теории хаоса, подтвержденной как в математических расчетах, так и в жизни. На настоящий момент еще не существует математически точного аппарата применения теории хаоса для исследования рыночных цен, поэтому спешить с применением знаний о хаосе нельзя.
Вместе с тем, это действительно самый перспективный современное направление математики с точки зрения прикладных исследований финансовых рынков. «Странность» хаотического аттрактора заключается не столько в необычном виде, сколько в тех новых свойствах, которыми он владеет.
Странный аттрактор - это прежде всего притягательная область для траекторий из окрестных областей. При этом все траектории внутри странного аттрактора динамически неустойчивы.
Иными словами, если представить предельное множество как «клубок» в фазовом пространстве, то точка, характеризующая состояние системы, будет принадлежать этому «клубку» и не пойдет в другую область фазового пространства. Однако мы не можем сказать, в каком месте «клубка» находиться точка в данный момент времени.
Положительный ляпуновский показатель
Одним из таких парадоксальных свойств является чувствительность к начальным данным. Проиллюстрируем это.
Выберем две близкие точки х'(0) и х"(0), принадлежащих траектории аттрактору, и посмотрим, как меняется расстояние d(t) = |x'(t) - x"(t) | со временем.
Если аттрактором является особая точка, то d(t) = 0. Если аттрактор - предельный цикл, то d (t) будет периодической функцией времени. Величина лямба называется ляпуновским показателем. Положительный ляпуновский показатель характеризует среднюю скорость разгона бесконечно близких траекторий. 
Однако исследования последних десятилетий показали, что есть класс детерминированных систем (даже сравнительно простых), поведение которых можно предусмотреть лишь на ограниченный период времени. У странного аттрактора через время две сначала близкие траектории перестают быть близкими.
Сколько угодно малая неточность в определении начального состояния нарастает со временем, и мы в принципе не можем дать «долгосрочный прогноз». Таким образом, существует горизонт прогноза, что ограничивает наши способности предвидеть.
Фрактальная структура
Другой интересной характеристикой хаотического режима является фрактальная структура. Геометрическая структура странного аттрактора не может быть представлена в виде кривых или плоскостей, или геометрических элементов целой размерности.
Размерность странного аттрактора является дробной, или, как принято говорить, фрактальной. Кроме того, странный аттрактор обладает свойством самоподобия. Сколько бы малую часть странного аттрактора мы не взяли, она имеет ту же структуру. Целое оказывается подобным сколь угодно малой части.