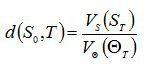Суть и способы линеаризации нелинейных динамических систем

1. Главная
2. Моделирование
3. Суть и способы линеаризации нелинейных динамических систем

Линеаразиция - один из наиболее распространенных методов анализа нелинейных систем. Идея линеаризации - использование линейной системы для аппроксимации поведения решений нелинейной системы в окрестности точки равновесия.

Линеаризация позволяет выявить большинство качественных и особенно количественных свойств нелинейной системы.

Методы линеаризации имеют ограниченный характер, то есть эквивалентность исходной нелинейной системы и ее линейного приближения сохраняется лишь для ограниченных пространственных или временных масштабов системы, или для определенных процессов, причем, если система переходит из одного режима работы в другой, то следует изменить и ее линеаризованную модель.

Линеаризация нелинейных динамических систем методом замены переменных

Линеаризация системы нелинейных уравнений в окрестности точки равновесия может быть достигнута путем замены переменных так, чтобы точка равновесия превратилась в начало координат.

Уравнения, полученные в результате указанного действия, будут линейными и называться линеаризацией исходной системы. Точки исходной системы, находящиеся в окрестности точки равновесия, будут соответствовать точкам в окрестности начала координат новой системы. Нас будет интересовать:

1. значение новых переменных, близкие к нулю;
2. при каких условиях нелинейными выражениями можно пренебречь.

Рассмотрим нелинейную систему: (1) что имеет точки равновесия (p, q). Преобразование u=x-p v=y-q переводит точки равновесия p, q в начало координат. Дифференцирование дает: (2) После замены переменных, подставив их новые значения в каждое уравнение, выделим линейную часть: где F(u,v) и G(u,v) и состоят только из нелинейных выражений. Говорят, что линейная система есть линерализацией системы (1) при таких условиях: Эти последние условия обеспечивают то, что нелинейные выражения F(u,v) и G(u,v) на столько малы по сравнению с u и v при приближении к точке равновесия, что ими можно пренебречь.

Линеаризация на основе якобиана

Замену переменных можно использовать и при другой организации линеаризации. Производят замену: где Это может быть записано в виде: где называется якобиан.