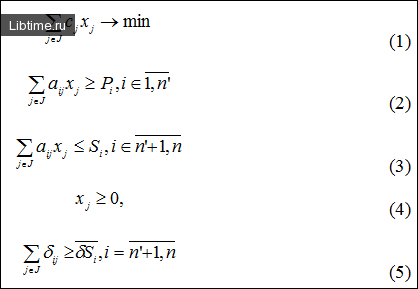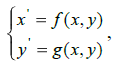Точки равновесия для динамических систем

1. Главная
2. Моделирование
3. Точки равновесия для динамических систем

Пусть имеем линейную однородную систему дифференциальных уравнений с постоянными коэффициентами: (1) Точки равновесия системы находят из решения системы: (2) Если определитель системы этой не равен нулю (3) то система имеет единственное решение. Тип положения равновесия определяется собственными числами матрицы системы, которые находят из характеристического уравнения: (4) где: - след матрици, - детерминант. Классификация точек равновесия в случае, когда Δ ≠ 0, представленная в таблице:

Классификация точек равновесия

Характер устойчивости положений равновесия

Собственные значения матрицы системы (1) однозначно определяют характер стойкости положений равновесия:

• Устойчивый узел - если действительные части всех корней уравнения (4) отрицательны, то точка равновесия системы (1)асимптотически устойчива.
• Седло, неустойчивый узел, неустойчивый фокус - если действительная часть хотя бы одного корня уравнения (4) положительна, то точка равновесия системы (1)неустойчивая.
• Центр - если уравнение (4) имеет чисто воображаемые корни, то точка равновесия системы (1) устойчива, но не асимптотически

Ниже изображены фазовые портреты динамических систем для каждого типа точек равновесия. Направление стрелок на фазовой кривой указывает направление движения фазовой точки при возрастании t. Неустойчивый диктрический узел: Устойчивый вырожденный узел: Неустойчивый вырожденный узел: Бифуркационная диаграмма позволяет определить тип точки равновесия.