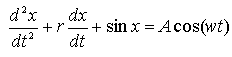Виды бифуркаций

1. Главная
2. Моделирование
3. Виды бифуркаций

Для изучения видов бифуркации желательно разобраться с самим понятием бифуркации.

В общем случае исследование всего фазового пространства на точки бифуркации является сложной задачей для n-мерного пространства, поэтому проводятся локальные исследования, а полученные точки бифуркации называются локальными точками бифуркации. За локальными точками бифуркации можно проследить, наблюдая развитие малых возмущений в системе Бифуркации состояний равновесия и периодических движений на примере шарика

Простейшими и наиболее важными из них являются бифуркации состояний равновесия и периодических движений.

Бифуркация положений равновесия

К основным бифуркациям состояний равновесия относят:

1. слияние и последующее исчезновение двух состояний равновесия. Примером может служить движение шарика в потенциальной «яме» с «полочкой» (рис. 1). При сглаживании «полочки» BD состояние равновесия «седло» S и центр С₂ сливаются и исчезают (рис. 2).

Рисунок 1 - Схема движения шарика в «яме» с «полочкой» (а) и его фазовый портрет (б) Рисунок 2 - Схема движения шарика после бифуркации (а) и его фазовый портрет (б)

• Рождение предельного цикла из состояния равновесия. Пример такой бифуркации бифуркация Хопфа.

Рассмотрим динамическую систему (1) Динамическаия система Она является упрощенным выражением сложной динамической системы, описываемой функциями x(t) и y(t), которые выражаются через соответствующие полярные координаты: и называется системой Хопфа. Система (1) зависит от двух параметров, один из которых λ будет для нас ключевым, а другой с=const.

Решения задачи Коши при некоторых заданных начальных значения r(t=0)=r₀, 'phi;(t=0)='phi;₀ при λ < 0 дает нам фазовый портрет и график динамики, изображенные на рис. 3. Рисунок 3 - График динамики (а) и фазовый портрет (б)

В данном случае существует единственная особая точка - устойчивый фокус.

Построим теперь график динамики и фазовый портрет для случая λ > 0 (λ = 4) (см. рис. 4) Рисунок 4 - График динамики (а) и фазовий портрет (б) при λ > 0

Разными цветами изображены развязки при различных начальных условиях. Как видим, после короткого переходного процесса система входит в колебательный режим, причем амплитуда и частота колебаний не зависят от начальных условий (при любых начальных условиях система придет в одно и то же колебательное состояние).

На фазовом портрете решение для разных начальных условий как бы «наматываются» на замкнутую кривую. Эта кривая, к которой при t -> ∞ стремятся решения задачи Коши, является аттрактором и называется предельным циклом.

Колебательный процесс, описывающий этот предельный цикл, называется автоколебаниями. Развязки в виде автоколебаний возможны только в существенно нелинейных динамических системах.

Динамическая система Хопфа имеет нелинейность в виде куба параметра, причем дополнительная нелинейность накладывается благодаря определению функций x(t) и y(t) как выражений тригонометрических функций. Можно доказать, что для данной динамической системы амплитуда колебаний равна . Итак, λ = 0 - бифуркационные значения параметра. В этой точке узел теряет устойчивость и вместо него рождается устойчивый предельный цикл.

Данная бифуркация рождения предельного цикла из неподвижной точки называется бифуркацией Хопфа, а рождение автоколебаний - мягким (при малых изменениях параметра колебания имеют малую амплитуду, которая увеличивается с его ростом).

Жесткое рождения автоколебаний - при малых изменениях параметра происходит «выброс» траектории в область притяжения другого аттрактора.

• Рождение из одного равновесного состояния трех состояний равновесия - спонтанное нарушение симметрии. Например, при движении шарика в желобе при условии появления в нем бугорка появляется бифуркация, при которой из вырожденного состояния типа «центр» возникают три состояния равновесия - седло S и центры С1 и С2 (рис. 5)

Рисунок 5 - Рождения из одного состояния равновесия трех при малом изменении параметра (формы желоба): а) форма желоба с одним минимумом и соответствующий фазовый портрет с одним состоянием равновесия типа «центр»; б) форма желоба с двумя минимумами и соответствующий фазовый портрет с тремя состояниями равновесия: «седло» S и «центры» С1 и С2

Бифуркации рождения (гибели) периодического движения

Всем бифуркация рождения или гибели состояний равновесия соответствует прохождение одного или нескольких корней через ноль. Такая возможность проиллюстрирована на рис. 5, где изображена гибель двух состояний равновесия типа «седла» и «узла».

Аналогичная бифуркация встречается в задачах о конкуренции видов Х1 и Х2, питающихся из одного источника. Соответствующая динамическая система, описывающая численность популяций, задается уравнениями: При ρ_1,2 > 1 в системе возможна «победа» одного из видов. При уменьшении любого из параметров ρ_1,2 до значения, меньшего от 1, при любых начальных условиях будет выживать только один вид (рис. 6, б). Рисунок 6 - Фазовые портреты численности популяций, а) при ρ₁ < 1, ρ₂ > 1; б) при ρ_1,2 > 1

Бифуркации смены устойчивости периодических движений

Весомая характеристика бифуркации устойчивости - значения мультипликаторов в критический момент, являющихся коэффициентами усиления (затухания) малых возмущений на фоне периодического движения за период Т.

В автономной системе один из мультипликаторов всегда равен единице, поэтому в дальнейшем говорим о других. Если все мультипликаторы по модулю меньшие единицы, то начальное периодическое движение устойчиво.

Бифуркации, связанные с исчезновением устойчивости, происходят при таких значениях параметров системы, при которых один или несколько из них равны по модулю 1.