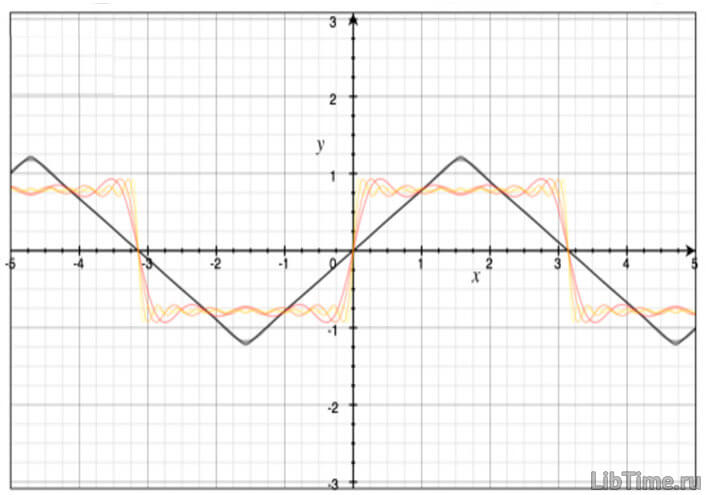
Зависимость результата развития экономического процесса от начальных условий и факторов влияния
Точного математического определения понятия хаос пока не существует. Сейчас зачастую хаос определяют как крайнюю непредсказуемость постоянного нелинейного и нерегулярного сложного движения, возникающую в динамической системе.
Следует отметить, что хаос не случаен, несмотря на свойство непредсказуемости. Более того, хаос динамически детерминирован (определен). На первый взгляд непредсказуемость граничит со случайностью - ведь мы, как правило, не можем предсказать именно случайные явления.
И если относиться к рынку как к случайным блужданиям, то это именно тот самый случай. Однако хаос не случаен, он подчиняется своим закономерностям. Согласно теории хаоса, если вы говорите о хаотическое движение, то вы должны иметь в виду не случайное движение, а другой, особенно упорядоченное движение.
Если динамика рынка хаотична, то она не случайна, хотя и по-прежнему непредсказуема.
Эффект бабочки
Непредсказуемость хаоса объясняется в основном существенной зависимостью от начальных условий. Такая зависимость указывает на то, что даже малейшие ошибки при измерении параметров исследуемого объекта могут привести к совершенно неверных прогнозов.
Эти ошибки могут возникать вследствие элементарного незнания всех начальных условий. То обязательно ускользнет от нашего внимания, а значит, уже в самой постановке задачи будет заложена внутренняя ошибка, которая приведет к существенным погрешностям в предсказаниях.
Применительно к невозможности делать долгосрочные прогнозы погоды существенную зависимость от начальных условий иногда называют «эффектом бабочки».
«Эффект бабочки» указывает на существование вероятности того, что взмах крыла бабочки в Бразилии приведет к появлению торнадо в Техасе.
Движение бильярдного шара
Дополнительные неточности в результате исследований и расчетов могут вносить самые на первый взгляд незаметные факторы воздействия на систему, которые появляются в период ее существования с начального момента до появления фактического и окончательного результата.
При этом факторы воздействия могут быть как экзогенные (внешние), так и эндогенные (внутренние).

Ярким примером хаотического поведения является движение бильярдного шара. От начальной точности удара, его силы, положения кия относительно шара, оценка месторасположения шара, по которому наносится удар, а также расположения других шаров, находящихся на столе, зависит конечный результат.
Малейшая неточность в одном из этих факторов приводит к самым непредсказуемым последствиям - шар может покатиться совсем не туда, куда ожидал бильярдист. Более того, даже если бильярдист все сделал правильно, попробуйте спрогнозировать движение шара после пяти-шести столкновений.
Рассмотрим еще один пример влияния начальных условий на конечный результат. Представим себе, например, камень на вершине горы. Стоит его чуть-чуть подтолкнуть, и он покатится вниз до самого подножия горы.
Понятно, что совсем малое изменение силы толчка и его направления может привести к очень значительному изменению места остановки камня у подножия. Есть, правда, одна очень существенная разница между примером с камнем и хаотической системой.
В первом факторы воздействия на камень во время его падения с горы (ветер, препятствия, изменения внутренней структуры вследствие столкновений и т.п.) уже не делают сильного влияния на конечный результат по сравнению с начальными условиями.
В хаотических системах малые изменения влияют на результат не только в начальных условиях, но и других факторах. Один из главных выводов теории хаоса, таким образом, заключается в следующем - будущее предсказать невозможно, так как всегда будут ошибки измерения, порожденные в том числе незнанием всех факторов и условий.
То есть, малые изменения и / или ошибки могут порождать большие последствия. 
Еще одним из основных свойств хаоса является экспоненциальное накопление ошибки. Согласно квантовой механике начальные условия всегда неопределенны, а согласно теории хаоса - эти неопределенности будут быстро прирастать и превысят допустимые пределы предсказуемости.
Второй вывод теории хаоса - достоверность прогнозов со временем быстро падает. Данный вывод является существенным ограничением для применимости фундаментального анализа, оперирующего, как правило, именно долгосрочными категориями.