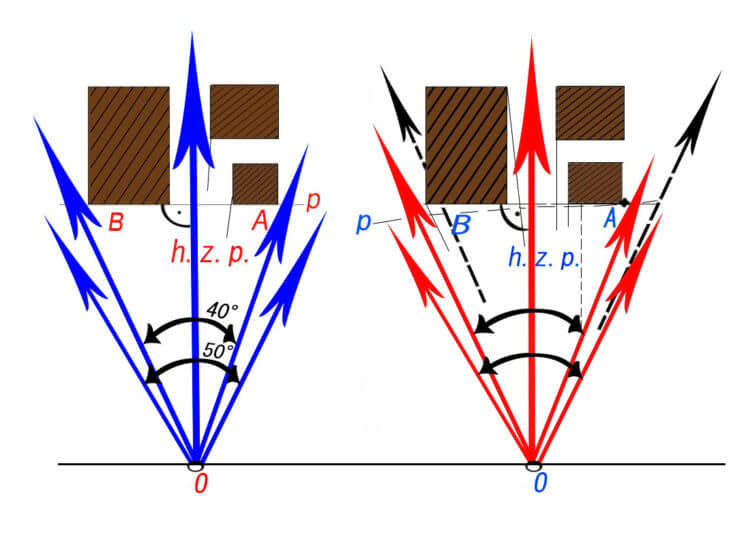
Рисование телеграфного столба
Если учащиеся еще не знают, как рисовать с натуры с подложенной бумагой и карандашом, они могут начинать изображение многогранных тел так, как описано ниже.
Рисование телеграфного столба и линии горизонта. 
Метод работы. Положение линии горизонта по отношению к столбу определяем сопоставлением расстояния АI и АВ в натуре. Если AI откладывается на линии АВ четыре раза, обозначаем соотношение 1 : 4.
Выполнение. Нарисуем отображение АВ произвольной длины. Разделим его в данном случае на четыре части. В точке I будет отражение искомой линии горизонта (рис. 1, Б).
Выполним еще одно задание.
Задание: определить и обозначить положение точки С к столбу АВ. Точка С находится ближе или дальше столба.
Метод работы. Это задание можно выполнять двумя способами. Первый способ быстрее, но менее точен. Выполняется он определением направлений АС и ВС и их нанесением. Вершина С является точкой пересечения обоих направлений.
Выполнение. Начертим произвольной длины отображение АВ. Направление АС определим с натуры и нанесем. Так же определим направление ВС. Точка пересечения обоих направлений и будет отображением искомой вершины С.
Второй способ точнее, но труднее.
Метод работы. Через вершину С проводим горизонтальную прямую. Потом определим расстояние СI сопоставлением с АВ. Здесь АI равна одной трети АВ, IС равна половине АВ.
Выполнение. Нарисуем произвольной длины отражение АВ. Разделим его на три части. В конечной точке нижней трети в отображении вершины I проводим горизонтальную прямую IС (рис. 1 Д). Длина CI равна половине АВ. Если вершина С ниже, чем А, проводим через вершину С горизонтальную прямую к. Потом определим соотношение между АI и АВ.
Если соотношение 1:3,5, разделим на рисунке АВ на три с половиной части. Одна целая часть будет искомой длиной AI. IС равна половине АВ.
Для обучения 7 способам перспективного рисования рекомендуется, кроме модели вращающегося круга, изготовить также модель вращающегося квадрата.