Нечеткая логика в экспертных системах. Апостериорная вероятность

Рассуждение, опирающееся исключительно на точные факты и точные выводы, исходящие из этих фактов, называются строгими соображениями. В случаях, когда для принятия решений необходимо использовать неопределенные факты, строгие рассуждения становятся непригодными.

Поэтому, одной из сильнейших сторон любой экспертной системы считается ее способность формировать рассуждения в условиях неопределенности так же успешно, как это делают эксперты-люди. Такие рассуждения имеют характер нестрогих. Можно смело говорить о присутствии нечеткой логики.

Неопределенность, а в следствии и нечеткая логика может рассматриваться как недостаточность адекватной информации для принятия решения. Неопределенность становится проблемой, поскольку может препятствовать созданию наилучшего решения и даже стать причиной того, что будет найдено некачественное решение.

Следует отметить, что качественное решение, найденное в реальном времени, часто считается более приемлемым, чем лучшее решение, для вычисления которого требуется большое количество времени. Например, задержка в предоставлении лечения с целью проведения дополнительных анализов может привести к тому, что пациент умрет не дождавшись помощи.

Причиной неопределенности является наличие в информации различных ошибок. Упрощенная классификация этих ошибок может быть представлена в их разделении на следующие типы:

• неоднозначность информации, возникновение которой связано с тем, что некоторая информация может интерпретироваться различными способами;
• неполнота информации, связанной с отсутствием некоторых данных;
• неадекватность информации, обусловленная применением данных, не соответствуют реальной ситуации (возможными причинами являются субъективные ошибки: ложь, дезинформация, неисправность оборудования);
• погрешности измерения, которые возникают из-за несоблюдения требований правильности и точности критериев количественного представления данных;
• случайные ошибки, проявлением которых являются случайные колебания данных относительно среднего их значения (причиной могут быть: ненадежность оборудовании, броуновское движение, тепловые эффекты и т.д.).

На сегодня разработана значительное количество теорий неопределенности, в которых делается попытка устранения некоторых или даже всех ошибок и обеспечения надежного логического вывода в условиях неопределенности. К наиболее употребляемых на практике относятся теории, основанные на классическом определении вероятности и на апостериорной вероятности.

Одним из старейших и важнейших инструментальных средств решения задач искусственного интеллекта является вероятность.

Вероятность - это количественный способ учета неопределенности. Классическая вероятность берет начало из теории, которая была впервые предложена Паскалем и Ферма в 1654 году. С тех пор была проведена большая работа в области изучения вероятности и осуществлении многочисленные применения вероятности в науке, технике, бизнесе, экономике и других областях.

Классическая вероятность

Классическую вероятность называют также априорной вероятностью, поскольку ее определение относится к идеальным систем. Термин «априорная» обозначает вероятность, что определяется «к событиям», без учета многих факторов, имеющих место в реальном мире.

Понятие априорной вероятности распространяется на события, происходящие в идеальных системах, склонных к износу или влияния других систем. В идеальной системе появление любого из событий происходит одинаково, благодаря чему их анализ становится намного проще.

Фундаментальная формула классической вероятности (Р) определена следующим образом:

P=W/N

В этой формуле W - количество ожидаемых событий, а N - общее количество событий с равными вероятностями, которые являются возможными результатами эксперимента или испытания. Например, вероятность выпадения любой грани шестигранной игральной кости равна 1/6, а извлечение любой карты из колоды, содержащей 52 различные карты - 1/52.

Аксиомы теории вероятности

Формальная теория вероятности может быть создана на основе трех аксиом:

1. Аксиома 1. В этой аксиоме утверждается, что областью определения вероятности события (Е) есть действительные числа от 0 до 1. Отрицательные значения вероятности не допускаются. Достоверной события присваивается вероятность 1, а невозможной события - вероятность 0:

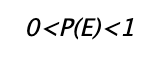
2. Аксиома 2. В данной аксиоме утверждается, что сумма вероятности всех событий, независимых друг от друга, что называются взаимоисключающими событиями, равно 1:

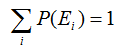
3. Аксиома 3. В этой аксиоме указано, что если события Е 1 и Е 2 не могут возникать одновременно (т.е. являются взаимоисключающими событиями), то вероятность возникновения того или иного события равна сумме вероятностей этих событий:

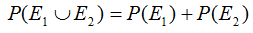
Приведенные аксиомы позволили заложить фундамент теории вероятности, однако в них не рассматривается вероятность событий, происходящих в реальных - неидеальных системах. В отличие от априорного подхода, в реальных системах, для определения вероятности некоторого события Р(Е), применяется способ определения экспериментальной вероятности как лимита распределения частот:

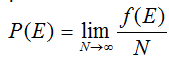
Апостериорная вероятность

В этой формуле f(E) обозначает частоту появления некоторого события между N-го количества наблюдений общих результатов. Вероятность такого типа называется также апостериорной вероятностью, т.е. вероятностью, определяемой «после событий».

В основу определения апостериорной вероятности положено измерение частоты, с которой возникает некоторое событие при проведении большого количества испытаний. Например, определение социального типа кредитоспособного клиента банка на основе эмпирического опыта.

События, которые не относятся к взаимоисключающих, могут влиять друг на друга. Такие события относятся к классу сложных. Вероятность сложных событий может быть вычислена путем анализа соответствующих им выборочных пространств.

Эти выборочные пространства могут быть представлены с помощью диаграмм Венна, как показано на рис. 1

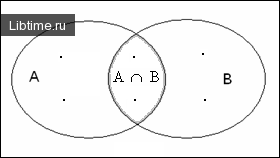
Рисунок1- Выборочное пространство для двух не взаимоисключающих событий

Вероятность наступления события А, которая определяется с учетом того, что произошло событие В, называется условной вероятностью и обозначается Р(А|В). Условная вероятность определяется следующим образом:

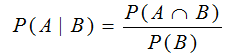
Априорная вероятность

В этой формуле вероятность Р(В) не должна равняться нулю, и представляет собой априорную вероятность, что определяется до того, как станет известна другая дополнительная информация. Априорную вероятность, что применяется в связи с использованием условной вероятности, иногда называют абсолютной вероятностью.

Существует задача, которая является по сути противоположной задачи вычисления условной вероятности. Она заключается в определении обратной вероятности, которая показывает вероятность предыдущей события с учетом тех событий, которые произошли в дальнейшем.

На практике с вероятностью такого типа приходится встречаться довольно часто, например, при проведении медицинской диагностики или диагностики оборудования, при которой выявляются определенные симптомы, а задача состоит в том, чтобы найти возможную причину.

Для решения этой задачи применяется теорема Байеса, названная в честь британского математика XVIII века Томаса Байеса. Байесивськая теория, в наши дни, широко используется для анализа деревьев решений в экономике и общественных науках.

Метод байесовского поиска решений применяется также в экспертной системе PROSPECTOR при определении перспективных площадок для разведки полезных ископаемых. Система PROSPECTOR приобрела широкую популярность как первая экспертная система, с помощью которой был открыт ценное месторождение молибдена, что стоимость 100 миллионов долларов.

Общая форма теоремы Байеса может быть записана в терминах событий (Е) и гипотез (Н), в следующем виде:

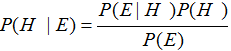
Субъективная вероятность

При определении вероятности события применяется также еще один тип вероятности, который называется субъективной вероятностью. Понятие субъективной вероятности распространяются на события, которые не являются воспроизводимыми, и не имеют исторической основы, с помощью которой можно было бы осуществлять экстраполяцию.

Такую ситуацию можно сравнить с бурением нефтяной скважины на новой площадке. Однако оценка субъективной вероятности, сделанная экспертом, лучшая, по сравнению с полным отсутствием оценки.

Субъективная вероятность, фактически, представляет собой убеждение или мысль, выраженную в виде вероятности, а не объективное значение вероятности, основанное на аксиомах и эмпирических измерениях. Убеждения и мнения экспертов выполняют важную роль в экспертных системах.