Предел текучести материала

Различные материалы по-разному сопротивляются пластической деформации, то есть изменению своей формы и размеров. Предел текучести материала - напряжения, при котором начинается пластическая деформация. Речь идет о силе, приходящейся на единицу площади. Измеряется это напряжение в Н/м²

или других единицах, имеющих размерность силы, деленной на площадь.

Изучение предела текучести материалов

Изучению предела текучести материалов уделяется пристальное внимание. В реальных конструкциях нагружать материал выше предела текучести нельзя, иначе вся конструкция изменит форму, размеры и потеряет работоспособность.

Предел текучести - это граница, переход через которую напряжениям, действующим в материале, запрещен. Естественно, что чем выше находится эта граница, тем большие нагрузки сможет выдержать конструкция. Вопрос о том, как управлять пределом текучести материалов - очень важен с технической точки зрения. Практически - это вопрос о работоспособности материала под нагрузкой.

Поэтому материаловеды издавна добросовестно испытывали различные материалы, вносили в справочники значения их пределов текучести после различных видов термической обработки и пластической деформации, а конструкторы использовали эти значения при расчетах несущей способности машин, самолетов, зданий, плотин.

Считалось, что определить предел текучести можно только экспериментально. А вопрос, почему предел текучести данного материала 100 МПа, а не 200 МПа, звучал странно. Что значит почему? Да потому, что природой так заложено.

Расчет величины предела текучести

Но вот в 1924 году известный советский ученый Яков Ильич Френкель решил рассчитать величину предела текучести теоретически. Идея расчета, как и все идеи Я. И. Френкеля в области физики, для которой он очень много сделал, была проста и понятна.

Он рассматривал процесс деформирования материала под действием сдвиговых напряжений. Чтобы вызвать пластическую деформацию, достаточно сдвинуть верхнюю половину образца относительно нижней так, чтобы возвращение в исходное состояние само по себе было невозможно. Как показано на рисунке. 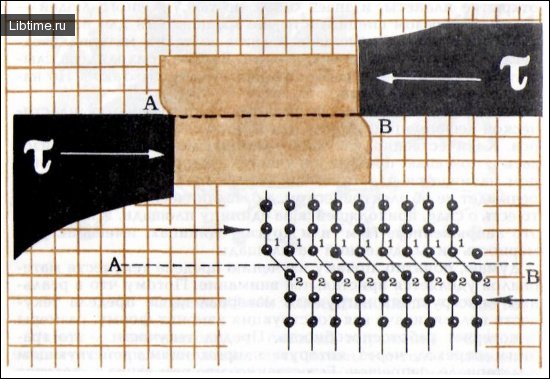Пусть рассматриваемый материал имеет кристаллическое строение (такое строение характерно для подавляющего большинства металлов, керамических, тугоплавких соединений, некоторых полимеров). Это означает, что его атомы расположены в определенном порядке, и если мысленно соединить их прямыми линиями, то получится пространственная решетка, которая полностью определит расположение атомов в кристалле.

Каждое вещество имеет характерные для него размеры и форму кристаллической решетки. Чтобы произвести пластический сдвиг в кристалле, нужно разорвать все связи между атомами, расположенными выше и ниже плоскости скольжения (ее след на рисунке - лини АВ).

При определенном напряжении равном пределу текучести кристалла при сдвиге, связи 1-2 разрушатся и тогда можно будет беспрепятственно сместить ряд атомов 1 относительно ряда 2 на одно межатомное расстояние. Такой сдвиг будет уже необратимым, то есть после снятия внешних нагрузок кристалл сам не вернется в прежнее состояние.

Точно такое же напряжение понадобится, чтобы произвести сдвиг еще на одно межатомное расстояние. Этот процесс будет повторяться до тех пор, пока все атомы 1 не придут в крайнее левое, а атомы 2 - в крайнее правое положение. После этого кристалл будет разделен на две части, то есть разрушится.

Величина предела текучести материала

Если прочность межатомной связи известна, то не составляет большого труда оценить величину напряжения, необходимую для того, чтобы пластически деформировать материал описанным способом. Я. И. Френкель проделал эти расчеты и получил простую формулу для оценки величины предела текучести материала τ_т: τ_т=G/2π.

В этой формуле G - модуль сдвига материала, связанный с прочностью межатомных связей. Значения модуля сдвига всех материалов, представляющих интерес для техники, имеются в справочниках. Например, для железа G = 81 ГПа, для никеля - 73,6 ГПа, для меди - 45,5 ГПа, для алюминия - 26,7 ГПа.

Следовательно, предел текучести при сдвиге должен составлять для железа ~ 13 ГПа, для никеля ~12 ГПа, для меди ~ 7 ГПа, для алюминия ~ 4 ГПа.

Противоречия между теорией и практикой

Теперь остается сравнить эти результаты с экспериментом. Нужно вырезать образцы металла и подвергнуть их испытаниям на сдвиг по схеме, изображенной на том же рисунке. Интересно, насколько ошибся Я. И. Френкель в своих расчетах.

Если даже в два-три раза, результат следует признать хорошим, учитывая приближенный, оценочный характер модели. Но оказалось, что реальные значения τ_т для железа и никеля вместо 12 000-13 000 МПа, предсказываемых теорией, составляют 50-100 МПа; меди - вместо 7000 МПа - 20- 30 МПа; алюминия - вместо 4000 МПа - 10-20 МПа.

Проверяем другие материалы. Та же картина. Теоретические значения предела текучести в сотни раз больше реальных. В чем же дело? Сомневаться в эксперименте у нас нет оснований. Значит, не верна теория. Но идея расчета так проста и естественна, что подозревать в ней какую-то ущербность не хочется. Может возникнуть вопрос - зачем вообще говорить о теории, если она не соответствует практике?

Есть экспериментально определенные значения предела текучести, их и следует использовать для нужд техники, а теория здесь ни к чему, тем более такая далекая от реальности. И все-таки нельзя пройти мимо полученных результатов. Причин тому несколько. Вот две из них.

1. До тех пор, пока не обнаружены принципиальные ошибки в теории, нет оснований ее отвергать. А раз теоретически возможно получение таких высоких показателей, то не исключено, что при определенных условиях они могут быть реализованы и на практике. Может быть, в материалах имеются еще неиспользованные резервы, о которых мы пока не знаем.
2. Без теории человек вообще не в состоянии осмыслить какой-либо экспериментально полученный результат. Альберту Эйнштейну принадлежат слова о том, что только теория решает, каково содержание наших наблюдений. Достаточно вспомнить, что повседневный опыт говорит нам: Земля стоит на месте, а Солнце всходит и заходит. А вот действительно ли это так или только кажется, выяснилось после того, как Коперник разработал свою теорию строения Солнечной системы.

Если нет надежной теории, которой можно руководствоваться, нет продвижения вперед.

Но вернемся к противоречию между теорией и практикой. Итак, как же было разрешено противоречие? Френкель оказался не прав. Материалы деформируются не так, как он себе представлял. Но его неправильные представления оказались для науки намного важнее и полезнее, чем многие заведомо правильные, но никуда не ведущие и никому не интересные.

Они заставили искать истину, и этот поиск привел к успеху. То, что Френкель был не прав, не совсем так. Его теория верна, но не для реальных, а для идеальных кристаллов, то есть таких, какими себе представляли металлы в двадцатые годы двадцатого века, когда ученый выполнял расчеты. Предполагалось, что кристаллическая решетка состоит из совершенно правильных рядов атомов и порядок их незыблем.

А на самом деле это не так. В кристалле имеются дефекты, и именно в них все дело. Такие разбежности в теоретических расчетах пределов текучести материалов и экспериментальных данных заключаются в дефектах кристаллических решеток. Чтобы объяснить разногласия между теорией и экспериментом, дефекты пришлось придумать. Сделал это в 1934 году английский физик Г. Тейлор.