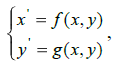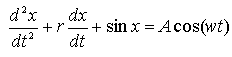Признаки катастроф
Рассмотрим признаки катастроф. О наличии катастрофы свидетельствуют специальные критические точки семейства потенциальных функций, которыми описывается система или явление. Однако такие точки часто не могут быть распознаны сразу.
Например, потенциальная функция является очень сложной или точно не известна. Еще хуже, когда система не является градиентной, и совсем плохо, когда нет даже туманных соображений о виде уравнения, адекватно тому, что описывает систему.
Однако, катастрофы часто встречаются в реальных ситуациях, и, следовательно, важно уметь их вовремя распознать. Катастрофы имеют отличительные особенности - признаки, которые позволяют привлечь внимание к данному процессу.
Как только зафиксирован один из них, т.е. установлен признак, свидетельствующий о наличии в системе катастрофы, управляющие параметры системы можно изменять так, чтобы найти и остальные признаки, которые при соответствующих условиях должны обязательно оказаться.
Установления наличия и типа катастрофы в случае неопределенности в описании системы помогает определить:
- упрощенную модельную потенциальную функцию, зависящую только от существенных переменных состояния и управляющих параметров;
- структурно устойчивую часть потенциальной функции, которая может подсказать, какой в действительности процесс имеет место;
- тип уравнения для системы и то, каким образом потенциальная функция в него входит;
- ненужность использования уравнений вообще.
Описание признаков катастроф
Модальность
Система может иметь два или более различных состояниях в некоторой области изменения управляющих параметров. Например, если управляющие параметры системы находятся в заштрихованной области, то система может находиться в трех различных состояниях (например, катастрофа сборки на рис. 1). 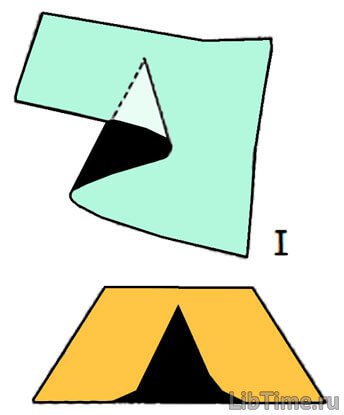
Недосягаемость
Существует область недосягаемых неустойчивых состояний равновесия, которой нельзя прийти, двигаясь по каким-либо устойчивых состояний. На рис. 1 срединный слой является недостижимым.
Катастрофические скачки
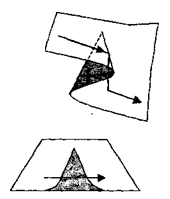
Малые изменения в значениях управляющих параметров могут вызывают большие изменения в значениях переменных состояния системы по мере того, как система перескакивает с одного локального минимума в другой, переход из окрестности одного локального минимума в другой оказывается в большом изменении значений изменением состояния, которое происходит в сверхбыстрой шкале.
На рис. 2 скачок происходит, как только состояние системы переходит из одного слоя поверхности катастрофы сборки на другой.
Расхождение
Конечные изменения в значении управляющих параметров приводят к конечным изменениям в значениях переменных состояния в точке равновесия. Обычно малые изменения в начальных значениях управляющих параметров ведут лишь к небольшому изменению начальных и конечных значений переменных состояния.
Однако при наличии катастрофы малые изменения начальных значений переменных состояния могут привести к большим изменениям конечных значений этих переменных. 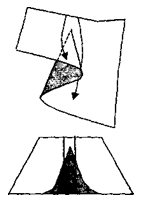
На рис. 3 показано, что траектории изменения управляющих параметров при близких начальных состояниях системы приводят к существенному отличию конечных состояний системы.
Гистерезис и необратимость
Гистерезис имеет место, когда процесс не является полностью обратимым. Прыжок с локального минимума 1 в локальный минимум 2 может не состояться при тех же значениях управляющих переменных, хотя прыжок с точки 2 в точку 1 имел место при движении в обратную сторону. 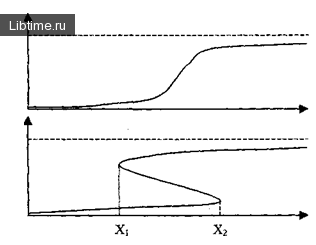
Рассмотрим зависимость эффективности труда рабочего и вознаграждения, за которую он работает. С увеличением вознаграждения эффективность труда также будет увеличиваться. Если вознаграждение не достаточно, то работник очень стараться.
С другой стороны, у каждого существует предел работоспособности, и, как бы ни повышалась вознаграждение, большего эффекта достичь не удастся. Эта ситуация примерно может быть описана функцией, изображенной на рис. 4.
Рассмотрим теперь динамический процесс, в котором оплата может повышаться и снижаться. Если в начальный момент оплата низкая, то эффективность работы также низкая. С повышением оплаты эффективность растет, но медленно, поскольку, по мнению работника, прирост оплаты недостаточен для увеличения эффективности работы.
Так будет происходить до момента Х2, когда дальнейший рост оплаты требует перехода на качественно новый уровень эффективности работы. Происходит скачкообразное изменение эффективности. Если, наоборот, в начальный момент времени оплата высокая, то эффективность поддерживается на высоком уровне.
В уменьшением оплаты происходит постепенное небольшое уменьшение эффективности (вступает в действие некоторая инерция, согласно которой человек продолжает работать в привычном ему режиме). Так происходит до тех пор, пока оплата не достигнет достаточно низкого уровня Х1.
В этот момент происходит резкое понижение эффективности, поскольку нет стимулов поддерживать ее высокий уровень. Фигура, изображенная на рис. 4б, называется петлей гистерезиса. Строго говоря, она не является функцией, поскольку одному и тому же значению X может соответствовать два (или даже три) значения У.
Наличие множества таких X - [Хр Х2] и приводит к возможности катастрофических изменений в состоянии системы. Само множество [Xt; Х2] называется бифуркационной множеством, т.е. такой, для значений параметров из которой возможно несколько различных состояний системы. На рис. 5 показано то же явление в трехмерной системе. 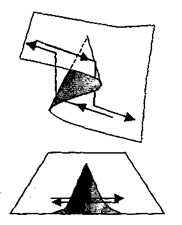
Итак, катастрофой называется резкое, скачкообразное изменение состояния системы при медленном изменении ее параметров (или управляющих переменных). Возвращаясь к примеру, можно заметить, что, если повернуть оси и рассматривать оплату как функцию эффективности, то мы имеем дело с полиномом третьей степени (рис. 4).
Этот полином не имеет экстремумов, а на рис. 4б имеет два экстремума. Очевидно, что количество экстремальных точек зависеть от коэффициентов полинома, т.е. параметров системы. Рассмотрим локальный характер потенциальных функций.
Свойства состояний равновесия зависят от вида и свойств потенциальной функции, которой описывается поведение системы. Ранее рассматривалась классификация состояний равновесия в двумерных системах, где оказались возможными 8 различных вариантов равновесия.
Если же переменных состояния системы больше, то полная классификация состояний равновесия оказывается весьма затруднительной.
Теория катастроф позволяет провести такую классификацию для достаточно широкого класса нелинейных систем.
Рассмотрим, какие преобразования возможны для потенциальных функций в окрестности состояния равновесия. Эти преобразования позволяют упростить функцию и привести ее к локально простого вида и выделить катастрофы. 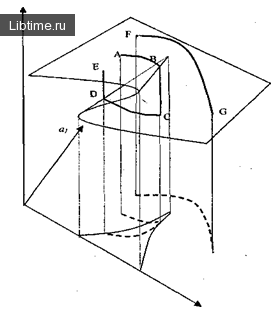
Как видно из рисунка, система, начинает свое движение из точки A, как можно дольше двигаться по верхней части поверхности, пока не достигнет множества сингулярности в точке В. Затем система совершает резкий скачок вниз в точку С и пойдет по нижней части поверхности.
Если система начинает свое движение на нижней части, то она пересечет бифуркационные множество в точке D и сделает резкий скачок на верхнюю часть поверхности. Возможна и другое поведение системы, которое не включает резких переходов.
Например, по траектории FG, если один из параметров системы также может быстро меняться. Экономические приложения теории катастроф во многом опираются на геометрические аспекты, в основном для описания экономического поведения применяется именно катастрофа сборки.
Другие элементарные катастрофы проиллюстрировать сложно, поскольку в них необходимо закрепление одного или нескольких параметров. Теория катастроф применяется для изучения многих проблем, включая крах фондовых бирж, поведение правительства, макромодели, структурные аспекты предположение Вальраса и др..