Выходные множества в планировании

Оптимизационные задачи планирования формируются на базе начального множества параметров и условий формирования плана.

Эти множества могут быть бесконечными или конечными. Их границы в значительной степени определяются состоянием объектов и ограничениями. Начальные множества могут быть подразделены на пассивные и активные. К пассивным относятся такие множества, которые не меняют своих границ и структуры при изменении системы ограничений и целевой функции.

Также к ним относятся такие множества, которые допускают изменения элементов, но эти изменения сводятся к дезагрегирования или агрегирования элементов исходного множества или к даче такой пассивной динамики элементов исходного множества, которая нейтральна по отношению к целевой функции и ограничений задачи.

Активными считаются следующие исходные множества, которые в зависимости от изменения ограничений или целей начинают (с присущими им маневренностью) менять свои границы и структуру так, что как только какой-либо начальной множества элементов приписаны некоторые внешние условия (ограничения, цели), оно обновится другим.

Положение двойственности доказаны для пассивных начальных множеств. Для активных множеств существует обратная связь между оценками, получаемыми в результате решения задачи на пассивной начальной множественном компонентами начального множества.

Динамику изменения границ начальной множества целесообразно отразить через влияние на них системы оценок. Такой подход будет наиболее адекватен, поскольку в реальной экономике система цен выполняет не только распределительные (по ресурсам), но и стимулирующие функции.

Под влиянием системы цен появляются новые технологии, технические способы, то есть в результате создается некая направлена активность. Направление этой активности будет определяться вектором оценок.

Что касается скоростных характеристик активности, т.е. например, темпов технического прогресса в тех или иных направлениях, то они зависят не только от вектора оценок, но и определяются маневренными свойствами в этой области (имеющийся научно-технический потенциал и ряд других обстоятельств).

Таким образом, через представление об активных начальные множества создается возможность формирования активного управления в оптимизационных задачах планирования, а система оценок начинает выполнять не только распределительную, но и стимулирующую роль.

Характер влияния оценок на начальное множество можно отображать на основе четырех различных подходов, в зависимости от меняющейся информации.

1. Если динамичность начальной активной множества примечательное, т.е. нельзя указать ни направления, ни границ изменения множества, то формирование оценок чрезвычайно важно, но теоретически их невозможно определить, и остается только использовать методы проб и ошибок.
2. Динамичность начальной множества может быть определена, но неопределенная: можно установить интервалы изменений, но законы распределения вероятностей таких изменений неизвестны.
3. Динамичность начальной множества может быть описана как категория достоверности.
4. Динамичность может быть описана детерминованоий, т.е. для фиксированной системы оценок можно предусмотреть все изменения, и эти изменения будут однозначными для каждого момента времени.

Переход от одного подхода к другому свидетельствует об изменении начальных концепций. Поэтому, если какие-либо выводы относительно оценок получены с применением одного подхода, то их формальное перенесение на другие подходы могут оказаться некорректным. При реализации данного подхода выделяются три этапа:

• изучение поведения плана как сложной системы при возможных изменениях начальной множества параметров и условий;
• определение основных направлений и областей существования новых путей развития системы,
• разработка методов и правил формирования планов на активных множествах,

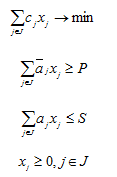
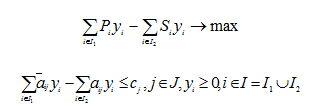
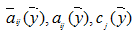
Рассмотрим математическую модель формирования плана, записанную в виде прямой и двойной задачи с неизвестными в общем случае параметрами Pj, Si - и переменными х_j, y_i. Нас будет интересовать поведение плана как системы на активном множестве параметров.

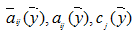
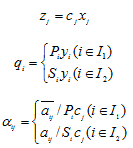
Анализ изменений множества и влияния этих изменений на решения оптимизационных задач удобно вести на множества однородных величин, однозначно выражаемых через начальные параметры Pj, Si. С этой целью введем новые переменные z_j, q_i и коэффициенты а_ij: Если с_j - удельные затраты на единицу интенсивности, то z_j - затраты на j-й объект (технологию). Расходы z_j непосредственно сравнимы между собой и в то же время выражают интенсивности затрат.

Величины q_j - суммарные оценки заданного количества необходимой i-той продукции. Расходные коэффициенты a_ij (i является I1) характеризуют удельные выпуски i-той продукции на единицу затрат j-гo способа в долях величины Р_i, а при (i является I2) - то же для i-го ресурса, потребляемого при j-м способе.

В этих переменных и параметрах прямая и двойственная задачи запишутся следующим образом: 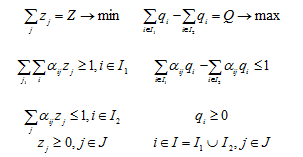Решение поставленной задачи предполагает нахождения соответствующего оптимального плана Z, вектора объективно обусловленных оценок q и значение целевой функции С.

При традиционном подходе из возможных способов определяется набор оптимальных, а способы с нулевыми интенсивностями отбрасываются.

При формировании плана на активных множествах этого делать нельзя, так как в определенных условиях эти способы могут или вытеснить некоторые начальные оптимальные, или стать постоянными для реализации необходимых изменений в способах с высокой оценкой.

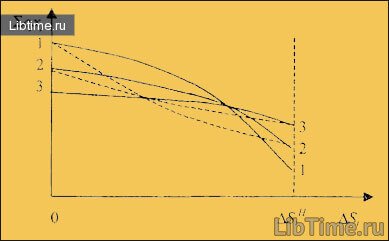
При заданных ограничениях в пространстве оценок q_i существует область V начальных допустимых планов, ограниченная поверхностью L₀ (рис. 1). 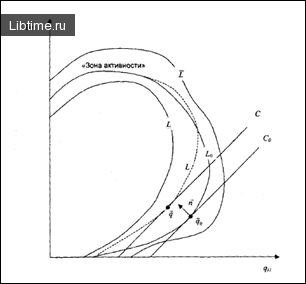Рисунок 1 - Изменение области допустимых планов при активных действиях: на начальную множество C₀ - гиперплоскость функционала, касательная к области начальных допустимых планов V в оптимальной точке q0 для пассивной начальной множества; С - гиперплоскость функционала, касательная к области начальных допустимых планов V в оптимальной точке q для активных множеств.

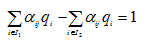
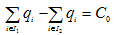
В линейной постановке это выпуклый многогранник, ограниченный гиперплоскости Для пассивного множества параметров граница L₀ определена однозначно (или в виде заданной функции времени) и оптимальный план соответствует точке касания этой границы гиперплоскостью Для активных множеств начальная граница L₀ является лишь некоторым возможным начальным состоянием системы.

Развитие плана на активных начальных множествах неизбежно должен привести к деформации границы области V, причем в определенной степени целенаправленной.

Так, стремление к росту эффективности производства за счет снижения издержек эквивалентно «давления» на область V в направлении нормали к гиперплоскости Q = sum(q_i). В результате начальное множество коэффициентов a_ij испытывать определенные изменения.

Наличие внутренних связей и ограничений, накладываемых на возможные пределы этих изменений, приведет к определенным противодействий, обусловленных инерционными свойствами системы, а также к передаче деформации на другие участки границы L.

В результате для каждого заданного горизонта планирования существовать некая «зона активности», в рамках которой может изменяться граница области существования решений (см. рис. 1). Выявление указанной зоны и поведения плана как сложной системы в ее пределах требует изучения структурных свойств плана, и в частности изучению взаимодействия элементов активных множеств.