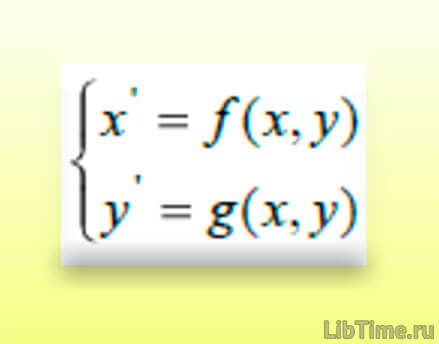Хаотический аттрактор. Хаос
Обычно говорят, что хаос является более высокой формой порядка, однако более правильно считать хаос другой формой порядка - с неизбежностью в любой динамической системе за порядком в обычном его понимании следует хаос, а за хаосом порядок.
Если мы определим хаос как беспорядок, то в таком беспорядке мы обязательно сможем увидеть свою, особенную форму порядка.
Например, дым от сигарет сначала поднимается в виде упорядоченного столба под влиянием внешней среды принимает все более причудливые очертания, а его движения становятся хаотичными.
Еще один пример хаотичности в природе - лист с любого дерева. Можно утверждать, что вы найдете много похожих листов, например дуба, однако ни одной пары одинаковых листьев. Разница определена температурой, ветром, влажностью и многими другими внешними факторами, кроме чисто внутренних причин (например, генетической разницей). 
Теория хаоса
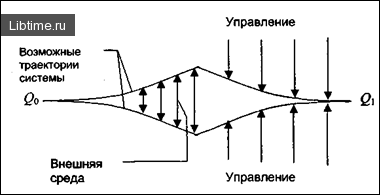
Движение от порядка к хаосу и обратно, по всей видимости, является сущностью Вселенной, способствующие проявлению ее мы не изучали. Даже в человеческом мозгу одновременно присутствует упорядоченное и хаотическое начала.
Первое отвечает левому полушарию мозга, а второе - правому. Левое полушарие отвечает за сознательное поведение человека, за выработку линейных правил и стратегий в поведении человека, где четко определяется «если ..., то ...».
В правом же полушарии царит нелинейность и хаотичность. Интуиция является одним из проявлений правого полушария мозга.
Теория хаоса изучает порядок хаотической системы, которая выглядит случайной, беспорядочной. При этом теория хаоса помогает построить модель такой системы, не ставя задачу точного предсказания поведения хаотической системы в будущем.
История теории хаоса
Первые элементы теории хаоса появились еще в XIX веке, однако настоящий научное развитие эта теория получил во второй половине XX века, вместе с работами Эдварда Лоренца (Edward Lorenz) из Массачусетского технологического института и франко-американского математика Бенуа Б. Мандельброта (Benoit B . Mandelbrot).
Эдвард Лоренц в свое время (начало 60-х годов XX века, работа опубликована в 1963 году) рассматривал, в чем возникает трудность при прогнозировании погоды. К работе Лоренца в мире науки господствовало два мнения относительно возможности точного прогнозирования погоды на бесконечно длительный срок.
Первый подход сформулировал еще в 1776 году французский математик Пьер Симон Лаплас. Лаплас заявил, что «... если мы представим себе разум, который в данное мгновение постиг все связи между объектами во Вселенной, то он сможет установить соответствующее положение, движения и общие воздействия всех этих объектов в любое время в или прошлом в будущем ».
Этот его подход был очень похож на известные слова Архимеда: «Дайте мне точку опоры, и я переверну весь мир».
Таким образом, Лаплас и его сторонники говорили, что для точного прогнозирования погоды необходимо только собрать больше информации о всех частицах во Вселенной, их местоположении, скорости, массе, направлении движения, ускорении и т.п. Лаплас полагал, чем больше человек будет знать, тем точнее будет его прогноз относительно будущего.
Второй подход к возможности прогнозирования погоды раньше всех наиболее четко сформулировал другой французский математик, Жюль Анри Пуанкаре.
В 1903 году он сказал:
«Если бы мы точно знали законы природы и положение Вселенной в начальный момент, мы могли бы точно предсказать положение той же Вселенной в последующий момент. Но даже если бы законы природы открыли нам все свои тайны, мы и тогда могли бы знать начальное положение только приближенно. Если бы это позволило нам предсказать последующее положение с тем же приближением, это было бы все, что нам нужно, и мы могли бы сказать, что явление было предсказано, что оно управляется законами. Но это не всегда так может случиться, что малые различия в начальных условиях вызывают очень большие различия в конечном явлении. Малая ошибка в первых породит огромную ошибку в последнем. Предсказание становится невозможным, и мы имеем дело с явлением, развивающийся по воле случая ».
В этих словах Пуанкаре мы находим постулат теории хаоса о зависимости от начальных условий.
Последующее развитие науки, особенно квантовой механики, опровергло детерминизм Лапласа. В 1927 году немецкий физик Вернер Гейзенберг открыл и сформулировал принцип неопределенности.
Этот принцип объясняют, почему некоторые случайные явления не подчиняются лапласовому детерминизму. Гейзенберг показал принцип неопределенности на примере радиоактивного распада ядра. Так, за очень малых размеров ядра невозможно знать все процессы, происходящие внутри него.
Поэтому, сколько бы информации мы не собирали о ядре, точно предсказать, когда это ядро распадется невозможно.
Инструменты теории хаоса
Какими же инструментами располагает теория хаоса. В первую очередь это аттракторы и фракталы.
Аттрактор (от англ. To attract - притягивать) - геометрическая структура, характеризующая поведение в фазовом пространстве в конце длительного времени. То есть аттрактор - это то, к чему стремится прийти система, к чему она притягивается.
Простейшим типом аттрактора является точка. Такой аттрактор характерен для маятника при наличии трения. Независимо от начальной скорости и положения, такой маятник всегда придет в состояние покоя, т.е. в точку.
Следующим типом аттрактора является предельный цикл, имеющий вид замкнутой кривой линии. Примером такого аттрактора является маятник, на который не влияет сила трения.
Еще одним примером предельного цикла является биение сердца. Частота биения может снижаться и возрастать, однако она всегда стремится к своему аттрактору, своей замкнутой кривой.
Третий тип аттрактора - тор. На рис. 1 тор показан в верхнем правом углу. 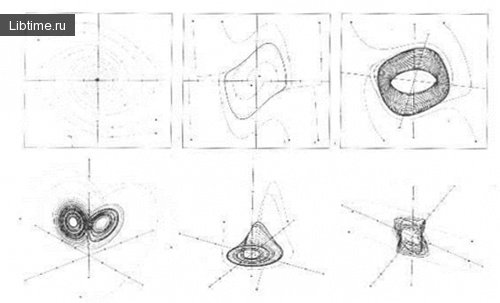
Вверху показаны три предсказуемых, простых аттрактора. Внизу три хаотических аттрактора.
Несмотря на сложность поведения хаотических аттракторов, иногда называемых странными аттракторами, знание фазового пространства позволяет представить поведение системы в геометрической форме и соответственно прогнозировать его.
И хотя пребывание системы в конкретный момент времени в конкретной точке фазового пространства практически невозможно, область нахождения объекта и его стремление к аттрактору предсказуемы.
Аттрактора Лоренца
Первым хаотической аттрактором стал аттрактора Лоренца. 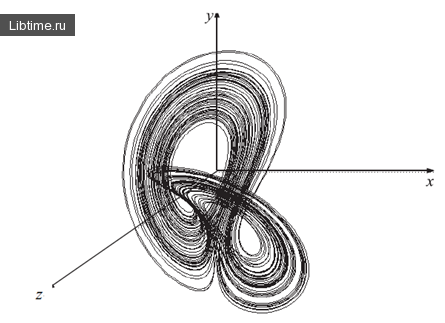
Аттрактор Лоренца рассчитан на основе всего трех степеней свободы - три обыкновенных дифференциальных уравнения, три константы и три начальных условия. Однако, несмотря на свою простоту, система Лоренца ведет псевдослучайных (хаотическим) образом.
Смоделировав свою систему на компьютере, Лоренц выявил причину ее хаотического поведения - разницу в начальных условиях. Даже микроскопическое отклонение двух систем в самом начале в процессе эволюции приводило к экспоненциального накопления ошибок и соответственно их стохастическом разногласия.
Вместе с тем, любой аттрактор имеет граничные размеры, поэтому экспоненциальная расхождение двух траекторий разных систем не может продолжаться бесконечно. Рано или поздно орбиты вновь сойдутся и пройдут рядом друг с другом или даже совпадут, хотя последнее очень маловероятно. Кстати, совпадение траекторий является правилом поведения простых предсказуемых аттракторов.
Сходимость-расхождение (говорят также, составление и вытягивание соответственно) хаотического аттрактора систематически устраняет начальную информацию и заменяет ее новой. При восхождении траектории сближаются и начинает проявляться эффект близорукости - возрастает неопределенность крупномасштабной информации.
При расхождении траекторий наоборот, они расходятся и проявляется эффект дальнозоркости, когда возрастает неопределенность мелкомасштабной информации. В результате постоянной сходимости-расхождения хаотического аттрактора неопределенность стремительно нарастает, что с каждым моментом времени лишает нас возможности делать точные прогнозы.
То, чем так гордится наука - способностью устанавливать связи между причинами и следствиями - в хаотических системах невозможно. Причинно-следственной связи между прошлым и будущем в хаосе нет.
Здесь же необходимо отметить, что скорость сходимости-расхождения является мерой хаоса, т.е. численным выражением того, насколько система хаотична. Другой статистической мерой хаоса служит размерность аттрактора.
Таким образом, можно отметить, что основным свойством хаотических аттракторов является сходимости-расходимость траекторий разных систем, что случайным образом постепенно и бесконечно перемешиваются.