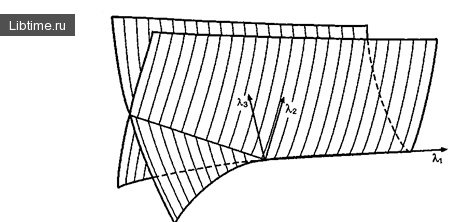
Предельный цикл системы

Среди решений нелинейных динамических уравнений особое место занимают решения, описывающие периодическую смену динамического состояния системы. На фазовой плоскости такому движению соответствует замкнутая траектория.

Изолированная замкнутая траектория на фазовой плоскости называется предельным циклом. Если все соседние траектории при приближаются к предельному циклу, то предельный цикл системы называется орбитально устойчивым (рис. 1а).

В случае удаления цикл называется орбитально неустойчивым (рис. 1б). Если траектория с одной стороны приближается к предельному циклу, а с другой удаляется, то предельный цикл называется полустойкий (рис. 1в). 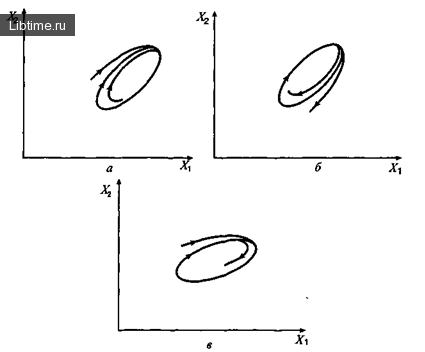Рисунок 1 - Фазовые траектории в окрестности предельного цикла

Наличие в системе предельного цикла свидетельствует о существовании периодических колебаний, частота и амплитуда которых не зависят от начальных условий. Предельный цикл системы

Андронов назвал их автоколебаниями. Они возникают при наличии положительной обратной связи в системе, а их частота определяется внутренними параметрами системы. Уравнения, описывающие автоколебания, называются нелинейными.

Часто для анализа устойчивости предельного цикла переходят к полярным систем координат. Однако, к сожалению, общих эффективных методов определения устойчивости предельных циклов не существует. Для исследования устойчивости предельных циклов используют функцию последования.