Случайные процессы и экономическая эволюция

Случайное поведение свойственно экономическим системам, описываются даже простыми дифференциальными уравнениями. При относительно простых взаимодействиях между экономическими переменными в системе могут быть эндогенно возбудимые регулярные и нерегулярные колебания.

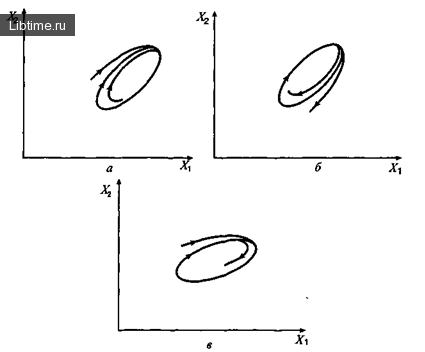
В хаосе есть имеющийся порядок. Однако есть и другой путь объяснения экономических флуктуаций: нерегулярное движение может возникать в системах, подверженных воздействию внешнего случайного фактора. Обратимся за примером к простому уравнению периодического движения маятника. 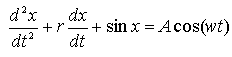где r - параметр затухания, А - амплитуда, w - частота силы, что вынуждает. Это уравнение решалось численно для различных наборов параметров (А, w, r), и на рисунке видно, что когда амплитуда А достигает определенной величины А0 изменения угла отклонения маятника х со временем выглядят просто хаотичными.

Начальные значения решения, приведенного на рисунке, равны x (0) = 0 и dx (0) / dt = 0, r = 0.2, а черные точки на рис.1 соответствуют тем значениям параметров (А, w), для которых движение маятника хаотичное. 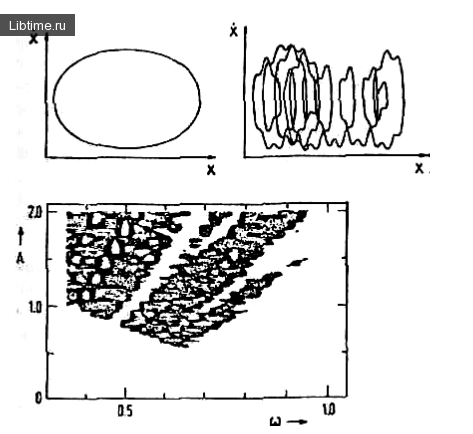Рисунок 1

Необходимость учета в экономике фактора шума отражает то обстоятельство, что некоторые события являются чисто случайными, вроде выигрыша в лотерее.

Считается, что экономические системы бывают часто подвержены воздействию окружающей среды. Такие действия распределены во времени и в пространстве случайным образом. Выигрыш в лотерею как пример случайного события согласно с учетом в экономике фактора шума. Другая точка зрения состоит в том, что даже если какие-то события - большой или малый урожай, изобретения и т.д. - в принципе, могут быть описаны на основе детерминированного механизма, с точки зрения экономики факт их появления является случайным.

Если основанием для принятия как приближение стохастической модели послужило последнее, то как только механизм будет обнаружен, модель должна быть заменена на детерминированную. Рассмотрим «стохастический подход» к вопросам экономической динамики и исследуем влияние на ход экономической эволюции малых флуктуации.

Макроэкономическая модель Лукаса

Характерный пример такого подхода к экономике можно найти в работе Лукаса (1975).

Макроэкономическая модель Лукаса базируется на системе линейных разностных уравнений с стохастическими членами. Экономика подразделяется на «острова» (области). Информационные потоки между различными островами неполные.

Эта географическая особенность означает, что когда агенты отмечают рост цен, они не могут сказать, выросли цены только на острове их заселения или повсеместно.

Таким образом, чисто номинальные колебания цен могут побудить людей к инвестициям средств, если они не знают реальных выгодных возможностей. Поскольку капитал, инвестированный в течение номинальных колебаний цен, неподвижный, эффект окажется лишь некоторое время спустя после возмущения.

Можно показать, что в рамках этой модели может быть возбуждены квазипериодических движение как цен, так и той части дохода, которая инвестирована. Это вполне разумно объясняет автокорреляции, наблюдаемые в макроэкономических данных.

Второй подход к объяснению нерегулярного движения сформулирован в результате изучения поведения детерминированных систем. Мы уже привели некоторые примеры такого подхода. В целом, он опирается на утверждение, что детерминированных уравнений и без учета каких-либо флуктуации достаточно для описания экономической динамики по двум причинам:

1. Флуктуации имеют малую интенсивность.
2. Флуктуации оказываются в более быстром по сравнению с макроскопическими уравнениями временном масштабе.

В этом разделе мы покажем, что подобная точка зрения справедлива только для некоторого ограниченного числа случаев. Даже флуктуации с нулевым средним значением способны сдвинуть систему далеко от равновесия; малые флуктуации могут вызвать структурную перестройку всей динамической системы.

Таким образом, флуктуациями в динамическом анализе пренебрегать нельзя. Следует подчеркнуть, что этот важный вывод относится только к неустойчивым динамическим системам, на которые сделан упор в нашем подходе к проблеме.

Возникает и другой вопрос: какой из подходов - основан на концепции неустойчивости или на концепции экзогенных шоков - только преобладающий при объяснении наблюдаемых нерегулярных флуктуации данных?

На этот вопрос в принципе невозможно ответить, опираясь только на исследование экономической модели, так как, в конце концов, оба подхода содержат существенные упрощения реальных экономических процессов. Однако мы должны сформулировать некоторые критерии для определения того, какой же подход и когда более приемлем.

Если принять за основу утверждение Фридмана (1953) о том, что в экономической модели реализм не является самоцелью, то нужно согласиться, что реализм должен присутствовать в модели в той степени, в которой модель сообщает нам об экономике что-то полезное.

Однако хорошая экономическая теория должна указывать на основной механизм, который вызвал то или иное экономическое явление. Исходя из этого, нельзя отдать предпочтение объяснению флуктуации в моделях делового цикла только на основе экзогенных шоков в ущерб пониманию их в терминах нелинейных взаимодействий между переменными.

Вместе с тем нельзя отрицать, что любая экономика подвержена случайных действий. Необходимость их учета является следствием нашего ограниченного понимания законов природы и других факторов. Например, мы не можем точно предсказать погоду, землетрясения и так далее.

Единственный способ учесть их в экономическом анализе - считать случайными. Существует утверждение, что только от характеристик системы зависит, вызовет случайный удар серьезные последствия. Для устойчивой системы, обладающий свойством быстро возвращаться к равновесию, действие внешнего удара будет незначительна.

Однако, как показано в этом исследовании, если система неустойчива, влияние случайных действий, даже если их средние значения равны нулю, очень сложный - это должно быть понятно из предыдущего анализа.

Мы показали, что неустойчивая система может претерпеть структурную перестройку даже в том случае, когда изменения параметров будут малы. Следовательно, можно интуитивно согласиться, что если система обладает «памятью», стохастический процесс даже с нулевыми средними может сместить систему далеко от невозмущенного равновесия.

Итак, чтобы предсказать поведение системы, нужно построить теорию флуктуации вблизи критических состояний.