Закон необходимого разнообразия в задаче планирования выпуска продукции

Для начала рекомендуется прочитать: Закон необходимого разнообразия.

Рассмотрим модель планирования, которая имеет вид: 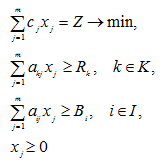(1) где: R_k - ограничение по выпуску продукции, диктуемые условиями рентабельности и обеспечения спроса на продукцию; S_i - ограничение по ресурсам и по продукции, связанные с ограниченностью сегмента рынка и деятельностью конкурентов; c_j, a_kj, a_ij - коэффициенты, характеризующие j-й объект планирования (способ производства, технологию, продукцию и т. д.); x_j - Интенсивность использования объекта.

В дальнейшем для определенности предположим, что объектом планирования является способ производства.

В частности, можно рассматривать эту задачу как задачу принятия решения о реализации одного из возможных бизнес-планов развития экономической системы. В таком случае интенсивности могут принимать только два значения {0,1}, а к задаче (1) необходимо добавить еще одно условие: 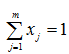Пусть в результате решения задачи (1) принят некоторый план x* = (x*₁, x*₂,...,x*_m). Заметим, что задача (1) всегда имеет решение, если только система ограничений совместима.

Целевая функция и правые части ограничений примут конкретные значения R*, S*.

Входами системы в соответствии с рис.1 есть ресурсы. Как было сказано ранее, различные воздействия внешней среды на систему могут быть сведены к недопоставкам ресурсов, совокупность которых выражается вектором ΔS = S* - S.

Выход системы характеризуется вектором продукции R. Управляющая система (U) формирует управляющие воздействия на систему для поддержки выпуска продукции в пределах норм эластичности или надежности.

Целенаправленность управления может выражаться различными функциями, зависящими как от состояния системы, так и от отклонения ее от заданного состояния. С точки зрения реакции системы на недопоставку ресурсов целесообразным есть критерий минимизации математического ожидания затрат.

Множество управляющих воздействий включает маневрирование интенсивности х, введение резервов (запасов), взаимозаменяемость ресурсов и другие действия, компенсируя недопоставки ресурсов. Закон необходимого разнообразия в задачи планирования выпуска продукции

Поскольку для данной системы целью управления является компенсировать недопоставку ресурсов и не допустить изменение в объемах выпускаемой продукции, то можно говорить о том, что управление однозначно реагирует на недопоставку, и условная энтропия управляющей системы равна нулю.

Поэтому закон необходимого разнообразия принимает вид H(R ) ≥ H(ΔS) - H(U), (2) где: H(ΔS) - энтропия разнообразия возможных значений вектора недопоставок ресурсов; H(R ) - энтропия разнообразия вектора выпусков продукции изменяется под влиянием недопоставок; H(U) - энтропия разнообразия возможных управлений, компенсирующих снижение выпуска продукции.

Интерпретацию предыдущего неравенства легко подать, если представить его таким образом: H(U) ≥ H(ΔS) - H(R), (3) откуда следует, что необходимый минимум разнообразия управления H(U), который должен быть заложен в план, при возможных внешних воздействий зависит от границы разнообразия выпуска продукции H(R ), соответствующего нормам эластичности (надежности).

Рассмотрим в связи с этим, как преобразуются требования эластичности (или надежности) плана в ограничении для разнообразия управления. Существенным предположением при использовании понятия энтропии является наличие информации о вероятности различных состояний системы.

В случае недопоставки ресурсов различные состояния внешней среды - это разные векторы недопоставок, каждый их которых характеризуется вероятностью его осуществления, т.е. совместной вероятностью недопоставок всех видов ресурсов p_i в их возможных комбинациях: p_i = p(ΔS_i).

Как было показано выше, энтропия достигает максимального значения, если события равновероятны, в данном случае равновероятными должны быть недопоставки различных количеств ΔS_i ресурса i.

Этот результат вполне соответствует реальной ситуации, действительно, чем больше неопределенность возможных значений недопоставок, тем ниже вероятность выполнения первоначального плана, даже если суммарное значение недопоставок одно и то же.

Если величина возможной недопоставки меняется в узких пределах, систему легче настроить на достижение заданных целей в условиях недопоставок ресурсов.

Итак, для того, чтобы снизить степень разнообразия H(AS), а значит и H(R ), и достичь стабильности выполнения плана, необходимо обеспечить такую структуру и маневренность системы, при малых значениях AS выпуск продукции был стабильным, чем при максимальных.

Это требование и может служить обоснованием нормативных кривых эластичности.

Роль энтропии существенно возрастает в перспективном, стратегическом планировании, поскольку в этом случае в наибольшей степени проявляется неопределенность исходных предположений задачи планирования.

Таким образом, использование энтропии как меры разнообразия (неопределенности) может оказаться весьма плодотворным для формализации задач оптимального планирования в условиях неопределенности исходной информации.