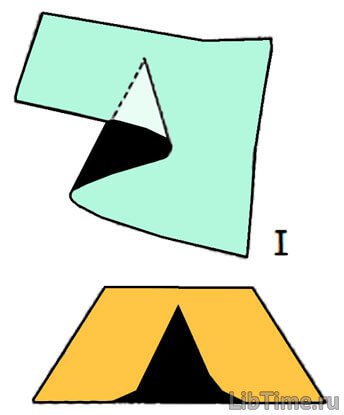
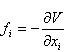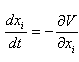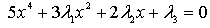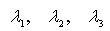Теория катастроф

В динамических системах возможна не только гладкое (непрерывное) и относительно предсказуемое поведение, но и резкие скачкообразные изменения. Такими скачкообразными изменениями в переменных состояния динамической системы занимается теория катастроф.

Хотя название предполагает исследование событий, сравнимых со стихийными катастрофами, эта теория имеет дело с менее эффектным поведением. В рамках данной теории рассматриваются вопросы как технического направления (переворачивание судов), социологического (внезапные вспышки агрессивности, бунтов), так и экономического (обвал фондового рынка). Переворачивание судов рассматривается как вопрос технического направления в рамках теории катастроф.

Понятие катастрофы

Потеря системой устойчивости называется катастрофой. Точнее же, катастрофа - это скачкообразное изменение, которое возникает при плавном изменении внешних условий. Выделяют и признаки катастроф.

Теория катастроф

Математическая теория, анализирующая поведение нелинейных динамических систем при изменении их параметров называется теорией катастроф. Теория катастроф определяет область существования различных структур, границы их устойчивости.

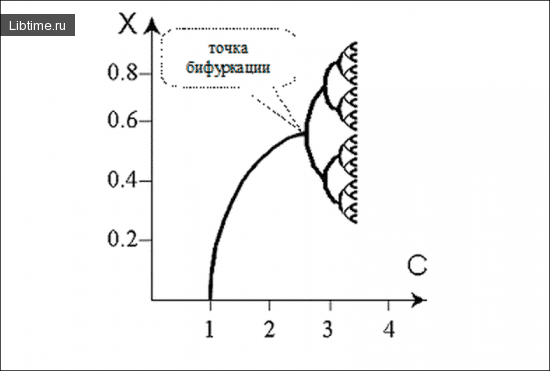
Для изучения же динамики системы необходимо знать каким образом новые "развязки" отходят от известного, что именно и рассматривает теория бифуркации. Момент перехода (катастрофический скачок) зависит от свойств системы и уровня флуктуаций. Теория катастроф сводит большое количество ситуаций к небольшому числу стандартных схем, которые можно детализировать.

Элемент теории катастроф

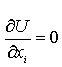
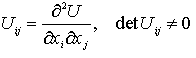
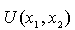
Элемент теории катастроф является в известном смысле обобщением задач на min и max в математическом анализе. Для функций одной переменной ее поведение определяется не вырожденным критическими точками - min и max (первая производная = 0, вторая производная != 0) Аналогично в многомерном случае для критических точек и отличный от 0 аналог второй производной . Невырожденные критические точки определяют min, max и седельные точки разного типа и дают качественную картину поведения потенциальной функции в многомерном случае. Так, функция напоминает рельефную картину: вершины гор и седла связаны хребтом являются озерными впадинами и седельными долинами. Если заполнить водой, то она соберется во впадинах.

Минимум, который притягивает воду называется аттрактором. Аттракторы имеют границе раздела между бассейнами притяжения. Это типичная картина рельефа (наличие только невырожденных критических точек).

Рассмотренная простая качественная картина существенно изменится при наличии вырожденных критических точек (одно или несколько значений 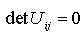). Равенство нулю возникает при некоторых определенных параметрах Са. Если с переменной Са система проходит вырожденные критические точки, топография коренным образом меняется (есть новый пейзаж). В этом смысле о переходе через новую точку говорят, как о катастрофе.

При приближении к границе перехода определенные критические точки рельефа сближается, а затем сливаются. Множество точек Са разбивает пространство управляющих параметров на открытые области. Каждой из этих областей соответствуют качественно отличные картины.

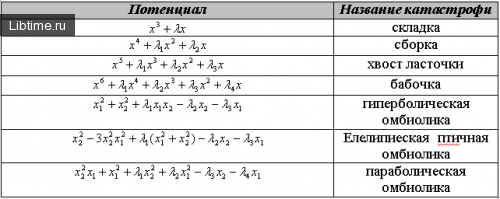
При пересечении границ, разделяющих эти области - сепаратрисы, происходит качественное скачкообразное изменение - катастрофа состояния системы. Цель - проанализировать на устойчивость функции вблизи вырожденных критических точек. Для одного или двух переменных и числа управляющих параметров, не превышающих 5 является 7 типов элементов катастроф. Таблица 1 - Элементарные катастрофы Потенциал V - это , а . Рассмотрим 3 случай. Особая точка определяется из условия: С изменением параметров число min и max меняется. В множестве это изменение происходит на бифуркационных поверхностях.