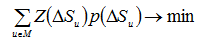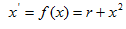Уменьшение энтропии в планировании

Один из возможных путей уменьшения энтропии H(R ) состоит в выборе при планировании таких видов и источников ресурсов, для которых энтропии H(ΔS_i), характеризующие разнообразие (неопределенность) обеспеченности ресурсами, имеют меньшие значения.

Однако такой подход, как правило, будет связан с ростом издержек, и, следовательно, ограничение, обусловленное законом необходимого разнообразия, должно быть в этом случае введенное в задачу оптимального планирования. Уменьшение энтропии в планировании

Второе направление - это использование целенаправленных управляющих воздействий на систему в ходе ее функционирования. Пусть в системе есть определенные возможности взаимозаменяемости ресурсов (или продуктов) при недопоставках.

В этом случае величины недопоставок AS не являются независимыми, поскольку есть возможность управления, т.е. активного действия на множество S_i и, в частности, снижение одних недопоставок за счет других или использование дополнительных ресурсов для снижения недопоставок других.

Из свойств вероятности следует теорема о сложении энтропии зависимых систем: для объединенных систем X и Y энтропия равна энтропии одной из ее составных частей плюс условная энтропия второй части по первой: H_c(X,Y) = H(X) + H(Y/X), где: H_c(X,Y) - энтропия системы со связями между подсистемами.

Условная энтропия системы не превышает ее собственной энтропии, т.е. H(Y/X) ≥ H(Y), причем равенство достигается только в случае, если системы независимы. Наоборот, если состояние одной системы полностью определяется состояние другого, то H(Y/X) = 0, H_c(X,Y) = H(X).

Таким образом, если есть две группы ресурсов, одна из которых может заменить другую, то чем больше возможности взаимозаменяемости, тем в большей степени можно снизить энтропию разнообразия вектора недопоставок H(ΔS), и, следовательно, увеличить стабильность системы.

Пример

Пусть система потребляет 3 ресурса в единичном объеме. Различают для каждого ресурса два принципиально разных состояния: 1 - ресурс поставляется полностью в необходимом объеме, 0 - ресурс недопоставленный. Тогда для всей системы поставок возможны следующие восемь разных состояний:

Если предположить, что все состояния системы равномерные, то энтропия данной системы равна: 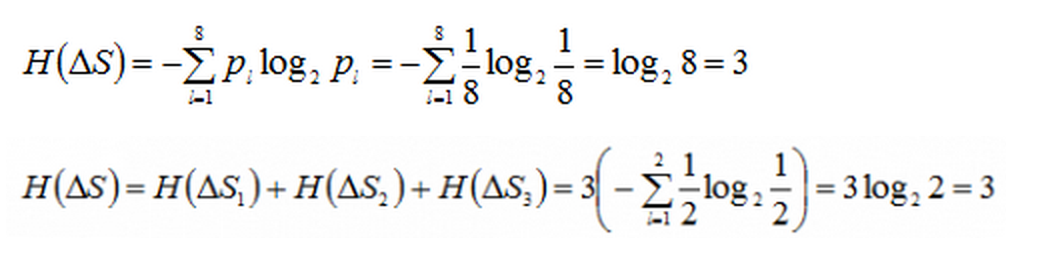Если недопоставка первого ресурса может быть компенсирована поставками второго или третьего ресурса, то состояния S2, S5, S6 могут быть исключены из рассмотрения, поскольку хотя в них ресурс 1 недопоставленный, поставки 2-го (в состоянии S6), 3-го (S5) или обоих ресурсов (S2) компенсируют его нехватку.

А вот состояние S8 исключить нельзя, поскольку в этом случае поставлены в нужном объеме все ресурсы. Таким образом, для системы с взаимозаменяемости оказывается всего пять возможных состояний, и ее энтропия равна 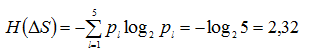Таким образом, использование взаимозаменяемости позволило улучшить систему, уменьшив ее разнообразие. Заметим, что использование как замена первого только одного какого-либо ресурса (второго или третьего), но не обоих вместе, позволяет сократить число возможных состояний на два, а энтропия системы в этом случае выше: H(ΔS) = log27 = 2,81.

Аналогично можно добиться снижения разнообразия недопоставок за счет введения резервов, увеличивающих возможности управления, т.е. H(U). Следующий способ управления предполагает возможность маневрирования интенсивности использования способов производства.

Если взаимозаменяемости ресурсов и использования ресурсов не компенсируют недопоставки какого-либо ресурса, то нужного объема выпуска можно достичь за счет изменения интенсивностей. Это означает, что каждому вектору недопоставки ΔS ставится в соответствие вектор изменения интенсивностей Δx. Для того, чтобы система была устойчивой по отношению к недопоставки, т.е. не нарушались условия ее существования, необходимо выполнение H(Δx) ≥ H(ΔS).

Это неравенство означает, что разнообразие маневра планируемой системы должно быть не меньше, чем разнообразие внешнего воздействия на систему. Однако этого недостаточно, чтобы обеспечить выпуск того же объема продукции.

Для этого необходим дополнительный резерв маневрирования, исходящий из закона необходимого разнообразия. Чем выше возможности маневрирования, тем, вообще говоря, больше возможности обеспечения стабильного выпуска и снижения затрат. Пусть правила маневрирования заданные ограничениями вида 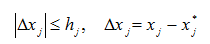В план х* вошли n составляющих с высокой маневренностью (т.е. с широким диапазоном Δx_j), а остальные составляющие плана обладает свойством высокой инерционности (весьма мало). Если при этом возможны недопоставки всех n ресурсов, то каждому ΔS будет однозначно отвечать x=x*-Δx, а значит и значения вектора R.

В результате будет иметь место равенство H(R ) = H(ΔS). Это равенство означает, что энтропия выпуска в точности равна энтропии внешних воздействий на систему, то есть ни система, ни управления не обеспечивают устойчивость решения.

Так, плановое решение должно иметь высокий уровень разнообразия управления H(U), в данной ситуации - разнообразие маневрирования. Очевидно, что повысить разнообразие маневрирования можно за счет введения в план (вместо одного или нескольких инерционных способов) высоко маневренных, ранее не вошли в план.

В этом случае возможно маневрировать так, чтобы обеспечить неизменность выпуска любого заданного вида продукции или, по крайней мере, обеспечить минимальное отклонение энтропии выпуска от нормативной. Целесообразный уровень маневренности плана связан также с минимизацией расходов, чтобы избежать чрезмерного разнообразия маневренности в задаче планирования необходимо ввести дополнительный критерий: Таким образом, вводя в план объекты с высокой маневренностью вместо способов с низкой маневренностью, формируется «ядро» эластичности и маневренности плана. Вместимость «ядра» эластичности определяется необходимым разнообразием маневрирования, а конкретный состав и величины компонент «ядра» - начальными условиями формирования плана свойствами маневренности его составляющих и нормами эластичности.