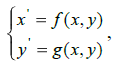Устойчивость предельного цикла системы

Пусть некоторая динамическая система задана уравнениями 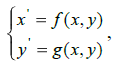Решение данной системы при t → ∞ не всегда задается состоянием равновесия.

Так, например, при условии получения мнимых корней соответствующего характеристического уравнения поведение системы характеризуется как незатухающие колебания с постоянной амплитудой, то есть решением являются функции x(t+T)=x(t), y(t+T)=y(t).

В данном случае говорят, что в системе существует устойчивый предельный цикл. Типичная картина поведения решений в окрестности предельного цикла представлена на рис. 1 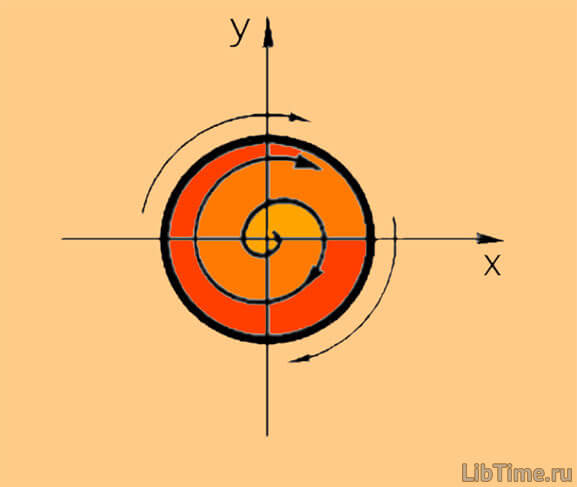Рисунок 1 - Устойчивый предельный цикл

Фазовые траектории изнутри и извне «наматываются» на цикл. Независимо от исходных данных в системе будут происходить колебания с постоянными амплитудой и частотой - так называемые автоколебания.

Типы предельных циклов:

• Устойчивые - близкие траектории «навиваются» на цикл при t → ∞ (рис. 2);
• Полустойкие - траектории, находящиеся по одну сторону от цикла - «навиваются» на него при t → ∞, а те, что находятся по другую сторону - «отходят» от цикла (рис. 3);
• Неустойчивые - близкие траектории «отходят» от цикла при t → ∞ (рис. 4).

Рисунок 2 - Устойчивые циклы; Рисунок 3 - Полустойкие; Рисунок 4 - Неустойчивые

К сожалению, обобщенных эффективных методов определения устойчивости предельных циклов не существует. Один из них основан на использовании функции подражания.

Функция подражания

Идея построения функции подражания состоит в следующем. Проводится луч, что явно пересекает предельный цикл и близкие траектории.

Например, проведем луч ОА, исходящего из особой точки О, которая лежит внутри предельного цикла (рис. 5). Введем координату r вдоль этого луча. Рассмотрим траекторию, выходящую из точки А, принадлежащей лучу.

Пусть эта траектория впервые пересекает луч в точке В. Введем функцию r_B = f(r_A), которая каждой точке с координатой r_A ставит в соответствие координату точки В. Пусть r_n - координата n-го пересечения траектории с лучом.

Тогда r_n+1=f(r_n), а предельном циклу соответствует неподвижная точка этого отображения r* = f(r*). Если r_n → r* для всех r_i, принадлежащих окрестности r*, то предельный цикл будет устойчивым. 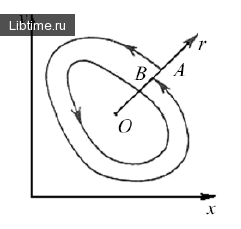Рисунок 5 - Построение функции подражания

Идея построения функции подражания оказалась очень плодотворной для исследования нелинейных систем, особенно высшего порядка (размерность фазового пространства N>2). Обобщение описанного подхода носит название метода сечений Пуанкаре.

При этом, переходя к системам с большим количеством измерений, вместо луча ОА следует рассматривать некоторую гиперплоскость. Например, в трехмерном случае рассматривают точки Р0, Р1, Р2, ..., Рn как сечения траектории с плоскостью S (рис. 6). Преобразования, что переводят точку в следующую, называется отображением Пуанкаре: Р_{n + 1} = Т(P_n) 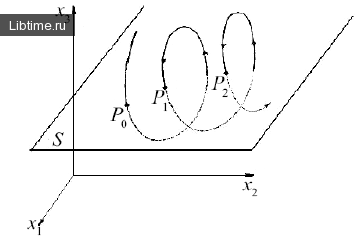Рисунок 6 - Схематическое изображение сечения Пуанкаре

Метод сечений Пуанкаре упрощает исследования непрерывных динамических систем по крайней мере по трем причинам:

• Количество фазовых переменных уменьшается на единицу;
• Дифференциальные уравнения заменяются разностными уравнениями вида x_i (k + 1) = f (x_i(k)), i = 1,2, ..., N, которые значительно легче поддаются исследованию;
• Резко сокращается количество данных, подлежащих обработке, так как почти всеми точками на траектории можно пренебречь.

Кроме того, многие системы дифференциальных уравнений порождают схожие отображения. Поэтому сейчас часто одномерные и двумерные отображения рассматриваются как упрощенные модели различных процессов.

Ознакомьтесь так же: Структурная устойчивость системы.