Бифуркации
Важная особенность социально-экономических систем - это то, что ими можно управлять, изменяя факторы, действующие на них.
Например, в уравнении q1=bq1q2 постоянная b описывает связь между двумя системами q1 и q2. Если силу связи регулировать снаружи, то b играет роль управляющего параметра. Итак имеем систему автономных дифференциальных уравнений. Автономная - явно не зависящая от времени t. 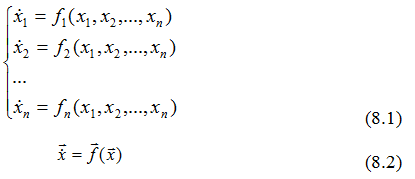

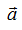
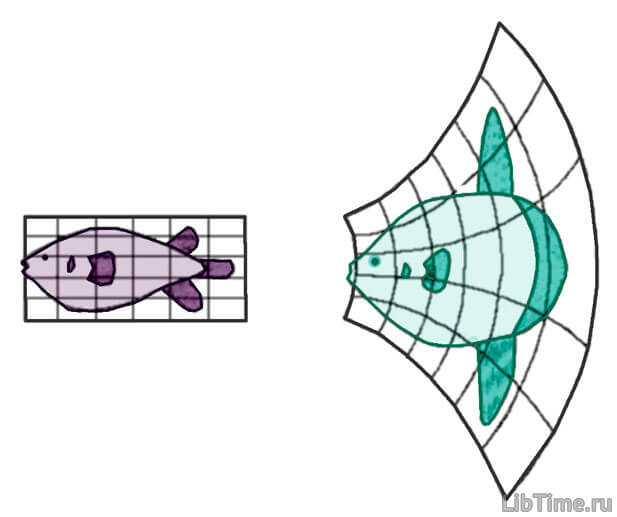
Каждый из двух рисунков только деформированная копия другого. В математической точке зрения две фигуры неотличим.
Другими словами, качественно новые свойства не возникает при деформации. То есть имеет место структурная устойчивость.
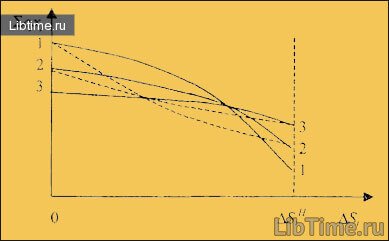
Качественное изменение фазового портрета называется бифуркацией. Даже незначительное изменение параметров 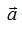
Пример
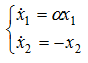
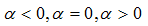
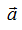
В общем случае, возможность исследования всего фазового пространства на точки бифуркации является сложной задачей для n-мерного пространства, этому проводятся локальные исследования, а полученные точки бифуркации - локальными точками бифуркации.