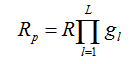Оптимальное решение по Парето

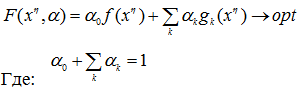
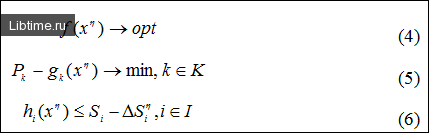
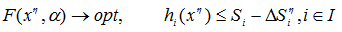
Оптимальное решение по Парето во многих практически интересных постановках может быть получено скаляризацией неотъемлемых коэффициентов целевых функций задачи Другими словами, задача (1) изменяется на одноцелевую: (2) Возможны и другие методы решения многокритериальной задачи. Принятие оптимального решения

Зависимость недовыпуска произвольного продукта 'Delta;Р от недопоставки какого-либо ресурса 'Delta;S можно рассматривать как частный случай платежной функции. Можно предположить, что она является выпуклой (кривая 1 на рисунке).

Предположение про выпуклость можно обосновать тем, что при небольших объемах недопоставок объект имеет относительно большие резервы их компенсации, а при очень больших недопоставках, когда все резервы исчерпаны, недовыпуск пропорционален объему недопоставок.

Поэтому ломаную 2 (см. рисунок) можно считать, с одной стороны, аппроксимацией кривой 1, а с другой - отрезок этой ломаной (0 - r) характеризует резервы, позволяющие объекту полностью компенсировать недопоставку.

Иными словами, r - эквивалент резерва типа запаса, по исчерпанию которого неизбежно происходит недовыпуск.

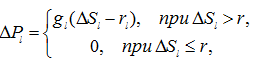
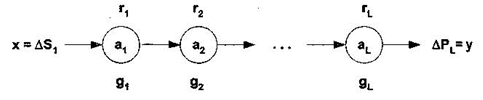
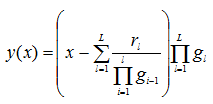
Предположим далее, что платежная функция произвольного 1-го объекта сложной системы имеет вид ломаной 2. В явном виде эту функцию можно записать так тогда для произвольноq L-этапной системы (цепочки) вида недовыпуск продукции последним (конечным) этапом этой цепи можно рассчитать по формуле (3) где: r - резерв объекта l; gl - коэффициент жесткости его функций эластичности; х - входное возмущение; y - недовыпуск продукции;

Легко увидеть, что при L=3 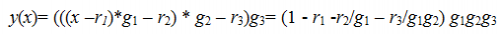Согласно этой формуле, от поступающего возмущение х вместе с резервом r; вычитается величина r₂ / g₁ + r₃ / g₁g₂.

Таким образом, величину R = r₁ + r₂/g₁ + r₃/g₁g₂ можно интерпретировать как полный резерв элемента а₁ или всей технологической трехэтапного системы. Величину r₂ / g₁ условно можно назвать «косвенным» резервом этой точки первого рода, r₃ / g₁g₂ - «косвенным» резервом второго рода.

Полный резерв всей технологической цепочки, при котором у(х) = 0, будет равен 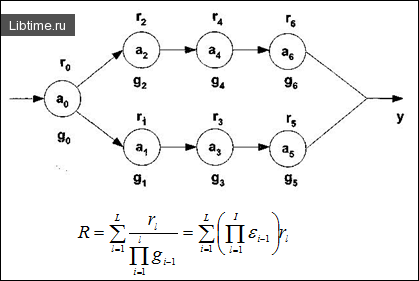(4) где 'epsilon;_i - коэффициент эластичности.

Можно указать формулу расчета полного резерва для вершины, из которой выходят несколько цепочек связей, например, для объекта а₀.

В общем случае для вершины а₀, из которой выходят m цепочек, начинающихся объектами а₁, а₂,..., а_M, полный резерв составит 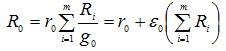, (5) где: R_i полный резерв цепочки, исходящий из элемента а₁; r₀ - резерв объекта а₀. Таким образом, формулы (4) и (5) позволяют рассчитать полные резервы любой точки технологически связанной системы.

Вместе с тем величина тоже есть полным резервом (то есть у(х)= 0), но решенная в единицах конечного продукта производимая последним L-м элементом.