Перспективная сетка

Художнику в своей практике особенно часто приходится иметь дело с обширными пространствами, на которых размещаются различные природные предметы (реки, озера, холмы, горы и т. д.). Поэтому особенно важна точная передача размещения видимых предметов, что обеспечивает перспективная сетка.

Знание законов перспективы позволяет решать и эти задачи с достаточной для наших целей точностью. Но здесь, особенно для начала, необходимо вооружиться некоторым терпением и проделать ряд необходимых упражнений.

Упражнение рисования карандашом для начинающих

Представьте себе обширную равнину, поверхность которой, подобно шахматной доске, разделена на квадраты, длина ребер которых равна 100 м. Нам, стоящим на некоторой высоте, необходимо изобразить на рисунке это поле.

Требуется изобразить не план поля, а именно рисунок, на котором каждый квадрат, в силу перспективных изменений, должен иметь различные размеры и различные очертания. Чтобы решить эту задачу, выбираем какой-либо один квадрат, находящийся прямо перед нами в расстоянии от нас, примерно, около 100 м. Мы уже имеем достаточный опыт рисования прямоугольников на полу, а потому без особенного труда с достаточной точностью строим этот квадрат АВСD (рис. 1, вверху).

Потом совмещаем линейку с передней, ближайшей к нам стороной квадрата и проводим линию, которая являлась бы продолжением этой стороны квадрата вправо и влево, т. е. продолжаем в обе стороны линию АВ. То же самое проделываем и с задней стороной квадрата (линия СD). У нас получатся две параллельные линии, которые определят положение всего первого ряда квадратов.

Продолжив боковые стороны нарисованного нами квадрата (АС и ВО) до их пересечения, мы получим точку схода, а следовательно, и местоположение линии горизонта. Передние стороны первого ряда квадратов лежат на линии АВ, и все они приблизительно равны.

Поэтому, если мы возьмем длину передней стороны нарисованного нами квадрата и отложим эту длину несколько раз вправо и влево по линии АВ, то получим местоположение всех передних сторон первого ряда квадрата. Соединив полученные точки с точкой схода, мы получим перспективные изображения всех квадратов первого ряда.

Все это совершенно понятно, потому что все боковые стороны квадратов параллельны и, естественно, они должны сходиться в одной точке схода на горизонте (рис. 1, снизу). 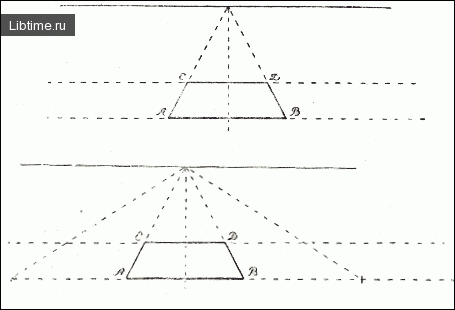Рисунок 1 - Рисуем объект в перспективе

Теперь проведем диагональ на первом изображенном нами квадрате (от точки А через точку D) и продолжим ее до пересечения с горизонтом. Эта линия в точке Е пересечет продолжение боковой стороны соседнего квадрата и тем самым определит местоположение задней стороны второго ряда квадратов.

Проводя через точку Е линию, параллельную линии СО, мы получаем изображение второго ряда квадратов (рис. 2, вверху). 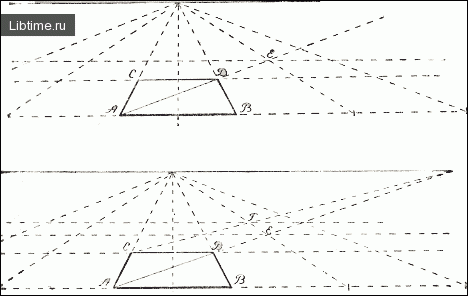Рисунок 2 - Пример рисования перспективной сетки

Далее берем квадрат второго ряда, расположенный как раз над первым нарисованным нами квадратом, и также проводим диагональ в точку схода (точка схода будет одна, ибо все диагонали квадратов тоже параллельны). Диагональ, пересекая продолжение боковой стороны квадрата в точке F, определяет положение задней стороны третьего ряда квадратов и т. д. (рис. 2, винзу).

Подобным образом мы определяем места четвертого, пятого и так далее рядов квадратов. Теоретически так можно строить ряды квадратов до самого горизонта, но практически их удается построить не более 6-7, так как далее, при нашей недостаточной точности черчения, будут уже значительные ошибки.

Даже построить 7-8 рядов квадратов возможно только при очень тщательной и точной работе. Но нам достаточно 5-6 рядов, чтобы убедиться в возможности геометрическим способом строить подобную перспективную сетку (рис. 3). Рисунок 3 - Рисуем перспективную сетку

Перспективная сетка - правила рисования

Полученная нами перспективная сетка имеет для нас огромное значение. Это мы поймем, как только проделаем ряд соответствующих упражнений. Но прежде чем подходить к этим упражнениям, заготовим несколько сеток, чтобы потом не отвлекаться от работы. Чтобы сетки были просты и удобны, мы предлагаем руководствоваться следующими соображениями:

1. Сетка чертится в размере не менее страницы тетради.
2. Линия горизонта должна совпадать с длиной, а не шириной листа.
3. Сначала проведите горизонт, потом точно по треугольнику вертикальную линию вниз чертежа. Далее откладываете вниз от горизонта по вертикали 6 см и проводите линию, строго параллельную горизонту. На этой линии как раз и будут располагаться передние стороны первого ряда квадратов.
4. На проведенной вами нижней горизонтальной линии вправо и влево от вертикали вы откладываете последовательно по 3 см. Далее вы соединяете эти точки с точкой пересечения вертикали и горизонта (с точкой схода).
5. По вертикали от нижней горизонтальной линии отметьте 1,5 см вверх и через полученную точку проведите параллельную линию. Так у вас получится перспективное изображение первого ряда квадратов.
6. Далее проведите диагонали в квадратах, примыкающих к вертикали справа и слева. Постарайтесь, чтобы они сошлись в одной точке на горизонте (точка будет близка к правому краю страницы).
7. Далее последовательно в ту же (правую) точку схода проводите диагонали и стройте последовательно остальные ряды квадратов.
8. Правильно построенная сетка обводится чернилами или тушью, а вспомогательные линии стираются. По этой сетке, путем накалывания, вы можете вычертить 10-15 сеток.

В дальнейшем, в целях экономии времени, перспективные сетки можно строить еще проще. Проделав все, что указано в пунктах 1, 2, 3 и 4, вы по вертикали снизу вверх откладываете последовательно сначала 2 см, потом 1,5; 1,0; 0,6; 0,4; 0,35; 0,3; 0,25 и 0,2. Через каждое из этих делений проводите горизонтальные линии, параллельные нижней.

Построенные нами перспективные сетки подойдут для изображения местности с некоторой довольно значительной высоты. Для изображения местности с меньшей высоты расстояние от горизонта до нижней горизонтальной линии должно быть меньше. Так, можно рекомендовать перспективную сетку, в которой от нижней горизонтальной линии до линии горизонта 4,2 см.

При этих условиях снизу по вертикали придется уже откладывать меньшие величины: для первого ряда 1, второго 0,6, потом 0,45; 0,3; 0,22; 0,17; 0,14 и 0,1. В дальнейшем нашем изложении первую сетку мы будем называть сеткой № 1, а вторую - сеткой № 2.

Сначала для наших упражнений возьмем сетку № 1. Ко всем дальнейшим упражнениям с перспективной сеткой мы даем рисунки подобные, но не являющиеся ответами на поставленные задачи.

Упражнение: построение перспективной призмы

Построить трехгранную удаляющуюся от вас призму, основанием которой является левая крайняя полоса квадратов. Высота призмы 0,5 стороны квадрата. Построенную призму разбить на отдельные призмы, основаниями которых являются отдельные квадраты (рис. 4). 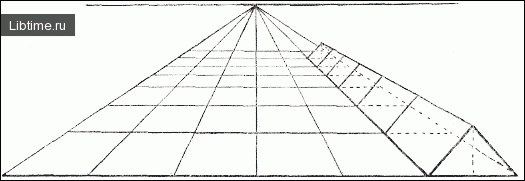Рисунок 4 - Построение удаляющейся от зрителя призмы

Упражнение: построение трех призм

Построить трехгранные призмы по трем удаляющимся полосам квадратов, но расположенные так, чтобы между основаниями призм оставалась полоса удаляющихся квадратов. Разделите призмы на части и покройте их склоны соответствующими штрихами (рис. 5). 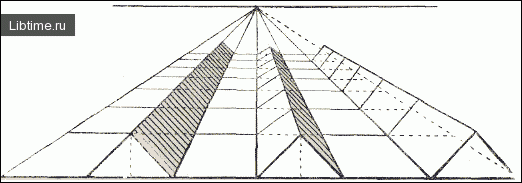Рисунок 5 - Построение ряда удаляющихся призм

Упражнение: построение пирамид

На крайней левой удаляющейся от вас полосе квадратов построить ряд пирамид, высота которых равна приблизительно половине длины стороны квадрата. Пирамиды располагаются не на каждом квадрате, а через квадрат. (Пересечение диагоналей в каждом квадрате дает точку, откуда следует проводить высоту. Определив вершину первой пирамиды, проводим от нее линии к точке схода. На этих линиях будут лежать высшие точки всех пирамид.)

Правые склоны пирамид покрыть соответствующими склонам штрихами (рис. 6). 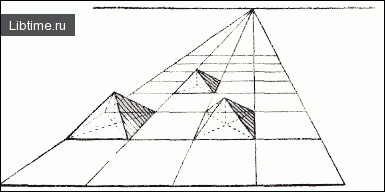Рисунок 6 - Построение пирамид

Построенные нами ряды призм и пирамид можно рассматривать как схему удаляющихся от нас хребтов или рядов разобщенных гор. Эти схемы легко превратить в параллельные ряды хребтов. На каждой призме или пирамиде, расположенной на 1 квадрате, мы изображаем вершину (рис. 7).

Упражнение: Рисование гор в перспективе

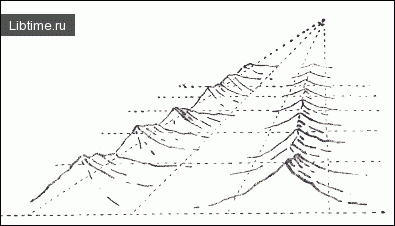
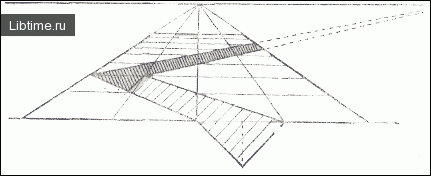
Возьмите сетку № 2 и постройте схему удаляющегося рва на правой, второй, считая от вертикальной линии, удаляющейся полосе квадратов. Глубина рва равна 0,5 стороны квадрата. Ров имеет вид врезанной трехгранной призмы (рис. 8). Рисунок 7 - Ряд удаляющихся хребтов, построенных на основе удаляющихся призм

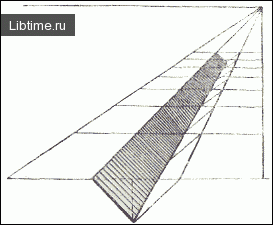
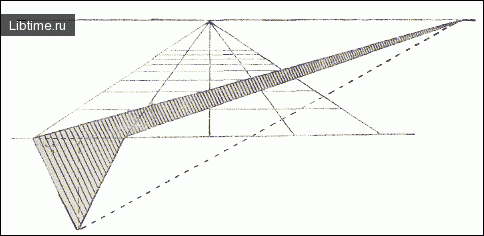
После этого, постройте схему подобного же рва, но идущего уже не по линии квадратов, а по диагонали. Ров начинается от первого левого квадрата, примыкающего к вертикали сетки. Глубина рва и сетки та же. Ров продолжается до горизонта. Левый склон покрыт штрихами (рис. 9). Рисунок 8 - Схема геометрически правильного удаляющегося рва Рисунок 9 - Ров удаляется по диагонали

Все дальнейшие упражнения с сеткой пойдут по сетке № 2.

Упражнение рисование перспективы

Построить схему рва, который начинается от левого квадрата, примыкающего к вертикали сетки. Ров идет на северо-восток до крайнего квадрата, а потом круто поворачивает на северо-запад и идет так до края сетки.

Сетка и глубина рва те же, что и в предыдущем упражнении (рис. 10). Зритель стоит лицом на север. Рисунок 10 - Схема двух пересекающихся рвов

Последние упражнения со рвом дают нам представление о построении рисунка оврагов (рис. 11).

Упражнение 16. Изобразите ряд одинаковых по высоте елей, идущих вдоль правой полосы квадратов до горизонта. Высота елей равна двум сторонам квадрата (рис. 12). 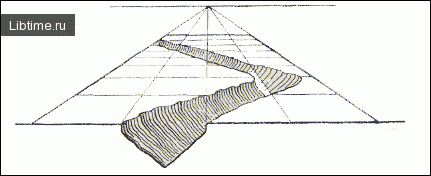Рисунок 11 - Перспективный рисунок оврага, построенного на основе двух геометрически правильных пересекающихся рвов Рисунок 12 - Схема удаляющихся рядов деревьев

Теперь на той же сетке (на предыдущем рисунке) слева рисуем ряд берез, но не на каждом квадрате, а через квадрат. Каждая береза должна быть в центре квадрата, а высота березы равна стороне квадрата (рис. 12).

Надеемся данный урок был Вам полезен. Регистрируйтесь на сайте и читайте Блог по рисованию.