Понятие бифуркации. Задачи теории бифуркаций

Исследование качественных математических моделей сопровождается возникновением качественных вопросов, можно разделить на две категории:

• Вопросы, относящиеся к поведению системы при фиксированных значениях параметров; важным при этом является качественное понимание характера режимов, устанавливаемых в системе;
• Вопросы, касающиеся событий, которые происходят в системе при изменении значений параметров. Медленное изменение параметра может привести к тому, что при пересечении некоторого критического значения режим, установившийся в системе, приобретает качественные изменения. При таких перестройках фазовый портрет изучаемой системы, изменяется. Качественные перестройки фазового портрета называются бифуркация.

Итак, вопрос второго типа предполагают определение бифуркационных значений параметров и описание явлений, происходящих при переходе через критические значения.

Задачи теории бифуркаций

Решением вопросов данного типа занимается теория бифуркации, задачами которой являются:

1. описание всех возможных бифуркации исследуемой системы;
2. разбиение множества бифуркационных значений параметров на области с разными типами грубых фазовых портретов;
3. построение для каждой области соответствующего фазового портрета.

Пример. Рассмотрим возникновение и сущность бифуркации. Пусть имеем динамическую систему, заданную уравнением 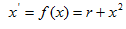Приравняем правую часть описания системы к нулю и проанализируем, какие значения может принимать параметр, т.е. как он влияет на поведение системы. Имеем уравнение: x²

= -r . (*) При r<0 уравнение (*) имеет положительную правую часть.

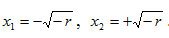
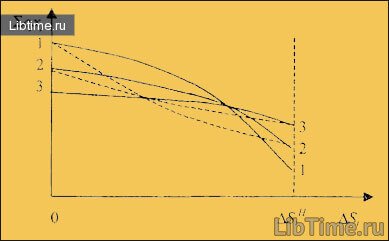
Итак, решений имеем два: 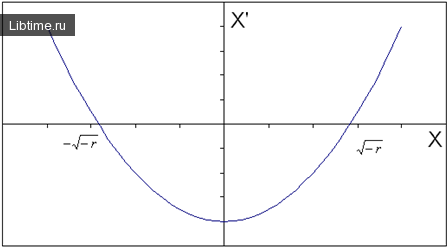Изобразим данный случай графически (рис. 1) Рисунок 1 - Поведение исследуемой системы в случае r<0

Первая точка (слева) устойчива, так как из рис. 1 видно, что функция меняет свой знак с «+» на «-». Вторая точка - неустойчива, так как из рис. 1 видно, что функция меняет свой знак с «-» на «+».

1. При r = 0 уравнение (*) имеет один корень. В этой точке, следовательно мы не можем аналитически определить тип устойчивости. Фазовый график представлен на рис. 2.

Рисунок 2 - Поведение исследуемой системы в случае r = 0

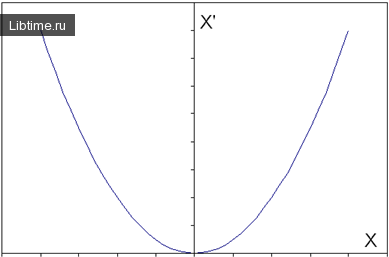
Из анализа графика рис. 2 можно установить, что функция f(x) при переходе через особую точку не меняет знак, следовательно эта точка является неустойчивой.

• При r > 0 точек равновесия нету:

0" loading="lazy"> Рисунок 3 - Поведение исследуемой системы в случае r > 0

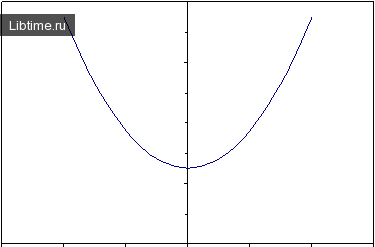
Итак, полустойкие точка равновесия исчезает, как только становится положительным. Так как характеристики точек равновесия меняются со временем, говорят, что динамическая система имеет бифуркацию.

В данном случае значение параметра меняются от отрицательных через ноль к положительным и характеристики стационарных точек изменяются так, как показано на рис. 1-3. Следовательно, в точке происходит бифуркация.

Точка бифуркации

Точка бифуркации - это такое состояние системы, при котором даже незначительное возмущение может привести к глобальным изменениям. Аналогично выражения «взмах крыла бабочки привел к урагану в Калифорнии».

Рыцарь на распутье - это точка бифуркация, космический аппарат, летящий между Землей и Луной и не имеющий необходимой скорости, чтобы выйти из гравитационного поля одной или другой планеты - точка бифуркации. Станет он спутником Земли или Луны, зависит от микроскопических возмущений типа солнечного ветра или микрометеоритов.

На фондовом и валютном рынках уровни поддержки или сопротивления являются точками бифуркации. Ценные бумаги или валюта, достигнув их, или сорвутся вниз, либо пойдут вверх и это зависит от очень незначительных факторов.

Август 1991 г. - точка бифуркации для СССР. Точи бифуркации часто встречаются в потоках газов и жидкости. Поэтому так трудно предсказать погодные условия. Предсказание погодных условий при помощи точек бифуркации

Термин «бифуркация» буквально означает «раздвоение», но применяется в более широком смысле для обозначения всех возможных качественных перестроек некоторого объекта при изменении параметра, от которого он зависит.

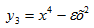
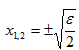
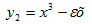
Существуют разные виды бифуркаций. В примере для функции значение параметра ε = 0 соответствует точке бифуркации, так как при переходе ε от отрицательных значений к положительным стационарное состояние х=0 стало неустойчивым и дополнилось парой устойчивых состояний - В примере при отрицательных значениях ε стационарные состояния вообще отсутствуют, а в точке ε = 0 происходит рождение таких состояний, один из которых устойчив, а другой - неустойчивый. В обоих случаях значения ε = 0 соответствуют точкам бифуркации, хотя и разных типов.

Проблемой исследования точек бифуркации является их классификация и анализ поведения семейств функций вблизи структурно неустойчивых особых точек.