Особые фазовые траектории узла и седла

Рассмотрим особые фазовые траектории узла и седла. Фазовая траектория узла

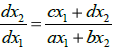
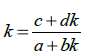
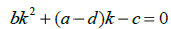
Если положение равновесия является седлом или узлом, то существуют фазовые траектории, лежащие на прямых, проходящих через начало координат. Уравнения таких прямых можно отыскать в виде x₂=kx₁ Если подставить это выражение в , то для определения k будем иметь: (1) Или

Описание фазовых траекторий

• Если корни уравнения k₁≠ k₂, то возможны два варианта:
  1. Седло: прямые x₂≠ k₁x₁ и x₂≠ k₂x₁ называют сепаратрисамы. Другие фазовые траектории - гиперболы, для которых найдены прямые являются асимптотами.
  2. Узел: прямые x₂≠ k₁x₁ и x₂≠ k₂x₁. Другие фазовые траектории - параболы, которые касаются в начала координат до одного из найденных прямых. Фазовые траектории касаются к той прямой, направленной вдоль собственного вектора, соответствующей меньшей по абсолютной величине λ.
• Если корни уравнения k₁=k₂, то тип точки равновесия будет вырожденный узел. Прямая x₂≠k₁x₁. Другие фазовые траектории - это ветви парабол, что касаются к этой прямой в начале координат.
• Существует только единственный корень k₁. Есть два варианта:
  1. Седло : прямые* x₂=k₁x₁ и x₁=0 - это сепаратрисы. Другие фазовые траектории - гиперболы, для которых найдены прямые являются асимптотами.
  2. Узел: прямые* x₂=k₁x₁ и x₁=0. Другие фазовые траектории образуют параболы, которые соприкасаются в начале координат к одной из найденных прямых.
• k - Любое число. В данном случае будем иметь доктрический узел. Все фазовые траектории находятся на прямых x₂=k₁x₁.

* Если уравнение прямых ищут в виде x₁=kx₂, тогда это будут прямые. Если положение равновесия является центром, то фазовые траектории являются эллипсами.