Структурная устойчивость системы

Рассмотрим функции y₁=x²

, y₂=x

и y₃=x

. Все они имеют единую стационарную (особую) точку x=0 (первые производные каждой функции обращаются в нуль в этой единственной точке). y₁ и y₃ имеют в этой точке минимальное значение, а y₂ - точка перегиба.

Введем в каждую функцию малые возмущения: 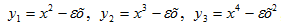где параметр ε может быть каким угодно малым. В результате примененного возмущения в первом случае никаких существенных изменений не произошло. Особая точка осталась одна, только ее значение сдвинулось на величину x₀ = ε/2 , а соответствующее значение y = ε²

/4 (рис. 1, а).

Для функций y₂ и y₃ ситуация совсем другая. Для y₂ особая точка с точки перегиба трансформировалась в две стационарные точки 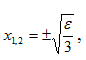одна из которых соответствует минимуму, а другая - максимуму (рис. 1, б). Функция y₄, которая имела единственный минимум в начале координат, в результате малого возмущения имеет уже три особые точки.

При этом начало координат является точкой максимума, а в двух других точках, сколь угодно близких к точке x=0, система принимает минимальные значения (рис 1, в). 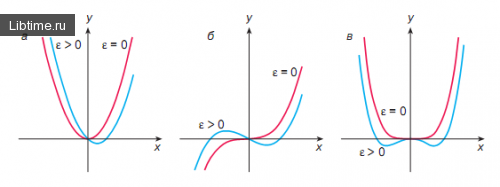Рисунок 1 - Деформация функции в окрестности особой точки при изменении параметра

Построение математической модели любого процесса связано со принебреганием маленькими членами. В первом примере (y₁) это вполне оправданно. Во втором и третьем примерах поведение функций при учете достаточно малых уточняющих членов существенно иная. Структурная устойчивость системы

Следовательно, функции и обладают свойством, что их объединяет, которая называется структурной неустойчивостью.

Соответствующая функция имеет свойство структурной устойчивости. Следовательно, срок структурной неустойчивости характеризует то, что при малом изменении структуры функции ее поведение в окрестности особой точки существенно и резко меняется.

Похожая статья: Устойчивость предельного цикла системы.