Концепции синергетики и самоорганизации формируют общий познавательный аппарат и позволяют выделить основные принципы синергетического подхода к моделированию. Наиболее существенное влияние синергетика […]
История понятия "Синтергетика" Суть понятия "Синергетика" - этимологически синергетика происходит от греческого «синергетикос» - совместный, согласованно действующий. На первом этапе развития под синергетикой […]
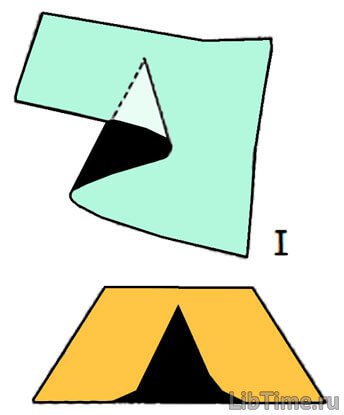
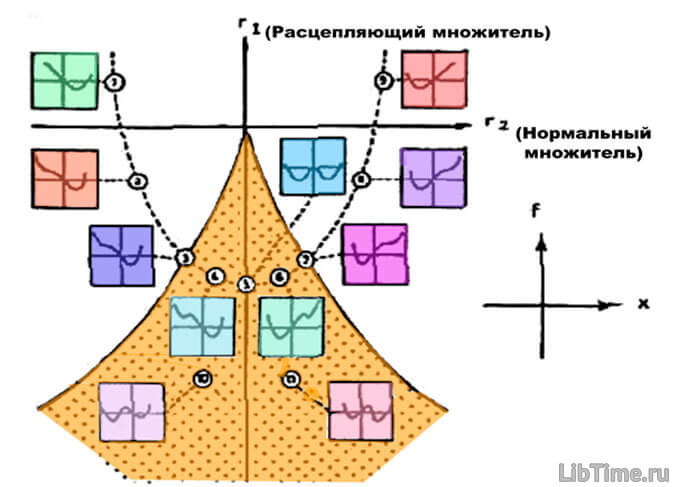
Рассмотрим признаки катастроф. О наличии катастрофы свидетельствуют специальные критические точки семейства потенциальных функций, которыми описывается система или явление. Однако такие точки часто не могут быть […]
Как рассматривалось в посте о бифуркационных поверхностях вне сборки есть только один корень, и он всегда отвечает минимуму потенциала f(x,r). Внутри области есть три действительных корня: один из них соответствует […]
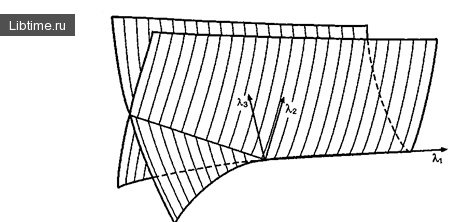
Рисунок 1 - Бифуркационные поверхности катастрофы типа "ласточкин хвост" Присутствие таких множеств и приводит к возможности катастрофических изменений в состоянии системы. Сама множество называется […]
В динамических системах возможна не только гладкое (непрерывное) и относительно предсказуемое поведение, но и резкие скачкообразные изменения. Такими скачкообразными изменениями в переменных состояния динамической […]
Фрактал как противоположность хаосу. Дерево Фейгенбаума
МоделированиеЗдесь проявляется пересечение фрактальной геометрии и теории хаоса. И, хотя одним из инструментов теории хаоса является фрактальная геометрия, фрактал - это противоположность хаосу. Фрактал Главное различие между […]
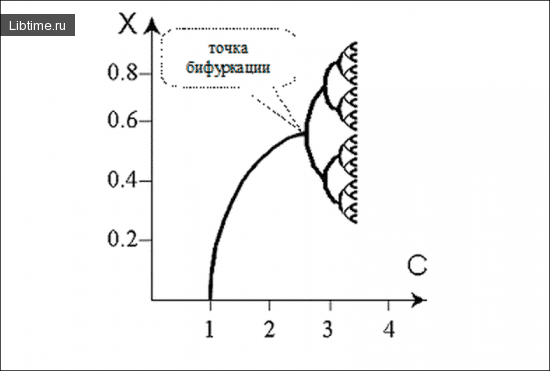
Переход к хаосу через бифуркации
МоделированиеК хаосу системы могут переходить разными путями. Среди последних выделяют бифуркации, что изучает теория бифуркаций. Бифуркация Бифуркация (от лат. Bifurcus - раздвоенный) представляет собой процесс качественного […]
Обычно говорят, что хаос является более высокой формой порядка, однако более правильно считать хаос другой формой порядка - с неизбежностью в любой динамической системе за порядком в обычном его понимании следует […]
Зависимость результата развития экономического процесса от начальных условий и факторов влияния
МоделированиеТочного математического определения понятия хаос пока не существует. Сейчас зачастую хаос определяют как крайнюю непредсказуемость постоянного нелинейного и нерегулярного сложного движения, возникающую в […]