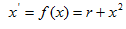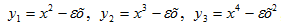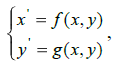Моделирование

Рассмотрим порядок взаимодействия системы с внешней средой, а так же источники неустойчивости планов. Поиск источников неустойчивости планов. Высказываемые принципы определения качества плановых решений в […]

Наибольшие возможности предоставляет экономическое маневрирование, особенно для долгосрочных программ развития. Свойства экономической инерции и обратные им характеристики возможного изменения управляющих […]

Рыночные отношения, во многом определяют условия функционирования и развития экономических систем в Украине и мире в целом, требуют весьма тщательной разработки всех управляющих мер и построения продуманных планов […]

Теория самоорганизации развивалась на основе динамики неравновесных процессов И. Пригожиным и его Брюссельской школой. Классическая термодинамика: рассматривает системы в состояниях равновесия или в их […]

Для изучения видов бифуркации желательно разобраться с самим понятием бифуркации. В общем случае исследование всего фазового пространства на точки бифуркации является сложной задачей для n-мерного пространства, […]

Исследование качественных математических моделей сопровождается возникновением качественных вопросов, можно разделить на две категории: Вопросы, относящиеся к поведению системы при фиксированных значениях […]

Рассмотрим функции y1=x2, y2=x3 и y3=x4. Все они имеют единую стационарную (особую) точку x=0 (первые производные каждой функции обращаются в нуль в этой единственной точке). y1 и y3 имеют в этой точке минимальное значение, а y2 - […]

Пусть некоторая динамическая система задана уравнениями Решение данной системы при t → ∞ не всегда задается состоянием равновесия. Так, например, при условии получения мнимых корней соответствующего […]

Часто динамические системы имеют оборотную во времени симметрию в том смысле, что их поведение не зависит от направления времени. Так, например, нить, на которой подвешен маятник, одинакова независимо от того, […]

Консервативные системы - это такие системы, в которых количество сохраняется в том смысле, что она постоянна на любой траектории системы. Часто хранения количества имеет физический смысл такой, как суммарная энергия в […]