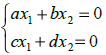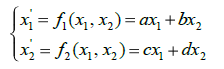Рассмотрим алгоритм построения фазового портрета линейных динамических систем: Определить положение равновесия, решив систему; Найти собственные значения матрицы системы из уравнения Определить тип точки […]
libre 4185
libre 4185
Направление движения по фазовых траекториях
Моделирование
Если положение равновесия является узлом или фокусом, то направление движения по фазовых траекториях однозначно определяется его устойчивостью (до начала координат) или неустойчивостью (от начала координат). […]
libre 7112
Особые фазовые траектории узла и седла
Моделирование
Рассмотрим особые фазовые траектории узла и седла. Фазовая траектория узла. Если положение равновесия является седлом или узлом, то существуют фазовые траектории, лежащие на прямых, проходящих через начало […]
libre 3495
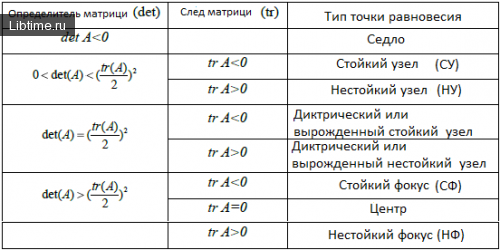
Бифуркационная диаграмма - можно определить тип точки равновесия и характер ее устойчивости, не находя собственных значений матрицы системы 1, а зная только ее след (tr) и детерминант (det). Тип точки равновесия и […]
libre 5134
Точки равновесия для динамических систем
Моделирование
Пусть имеем линейную однородную систему дифференциальных уравнений с постоянными коэффициентами: (1) Точки равновесия системы находят из решения системы: (2) Если определитель системы этой не равен нулю […]
libre 26586
Основные положения синергетики
Моделирование
Основные положения синергетики, как известно, в основе системного анализа лежит принцип системности, а в основе теорий самоорганизации - принцип развития. Оба принципа взаимодополняют друг друга и в действительности […]
libre 6187
Адаптационный и бифуркационный механизмы развития
Моделирование
В реальности процесс развития является единственным, сочетающим в себе различные механизмы. Основные черты единого процесса развития следующие. Законы природы устанавливают определенные пределы изменения […]
libre 4870
Параллельно с синергетическим исследованиями развивалась и теория самоорганизации на основе термодинамики неравновесных процессов. Фундаментальные результаты, полученные в исследовании термодинамики […]
libre 2014
Вкратце опишем открытые с помощью системного подхода и концепций самоорганизации закономерности развития национальной экономики. Закономерности развития национальной экономики Развитие экономики представляет […]
libre 3196
Основные положения концепции самоорганизации
Моделирование
Системы и их компоненты подвержены флуктуациям (колебаниям, изменениям, возмущением), которые в равновесных, закрытых системах гасятся сами по себе. В открытых системах под воздействием внешней среды внутренние […]
libre 3852